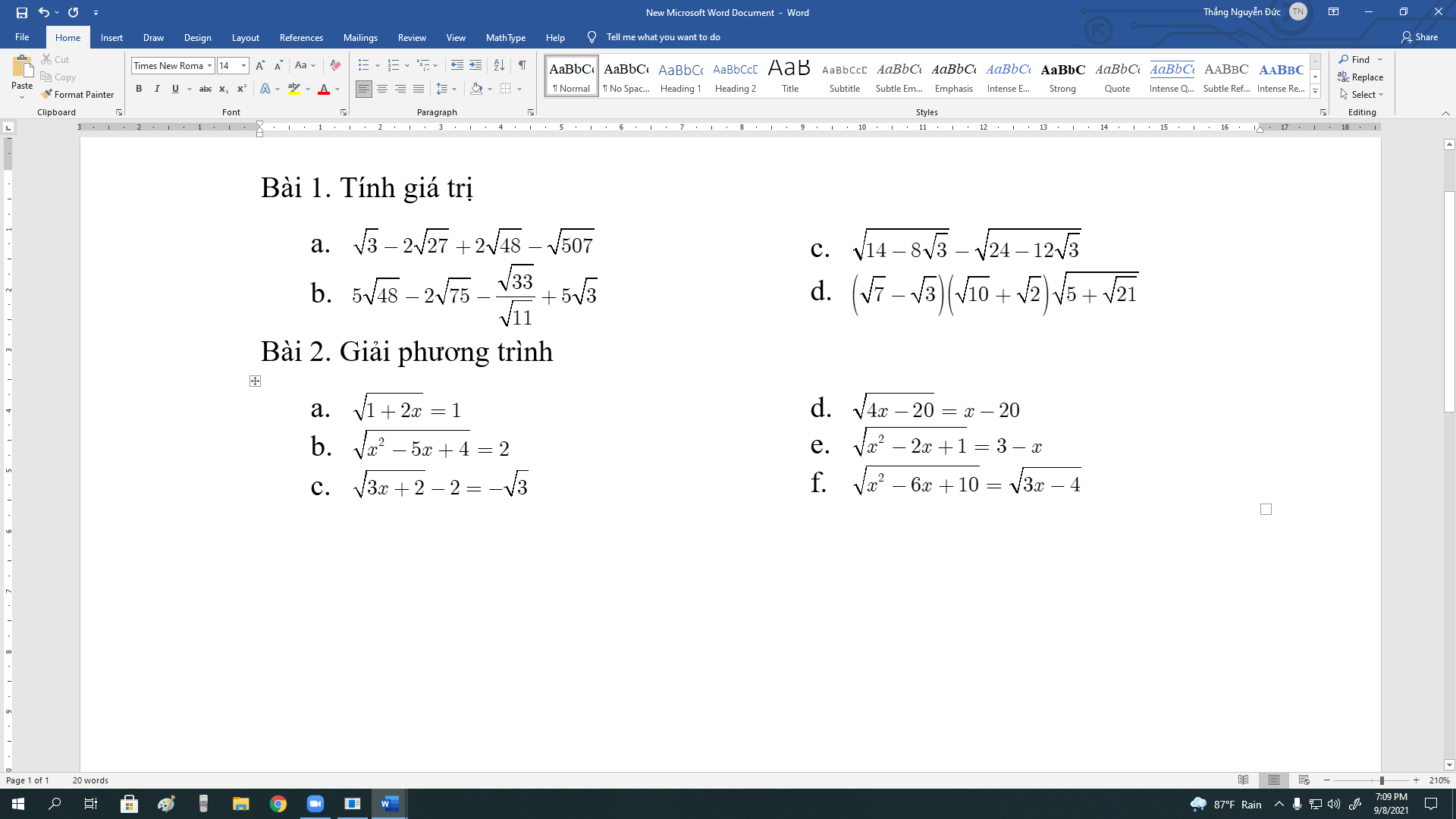
mình cần gấp câu 1 cảm ơn
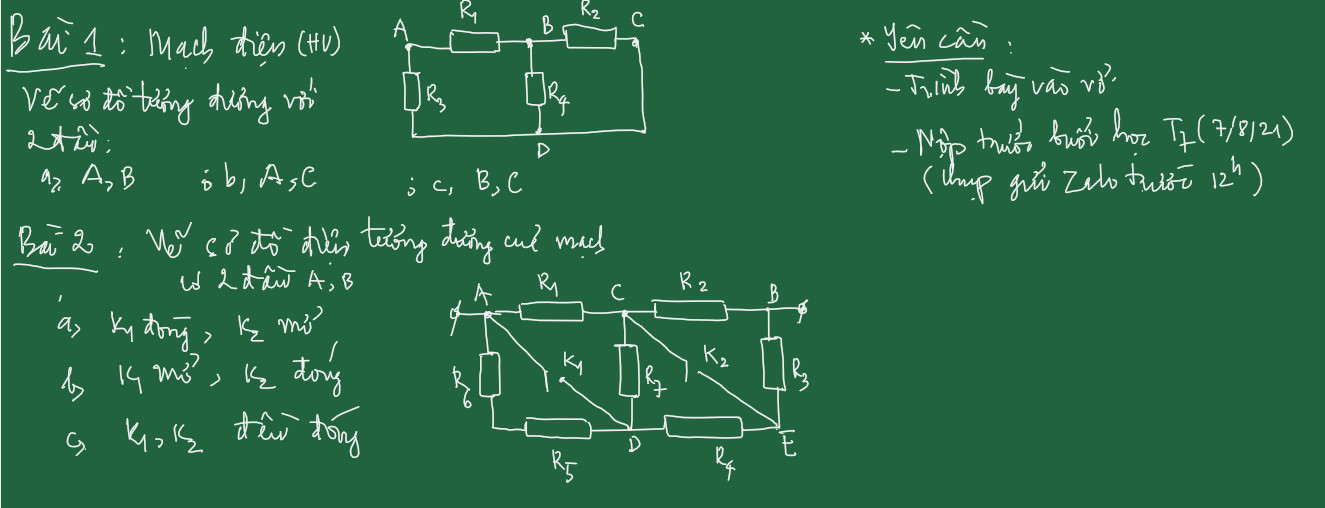
làm câu 1 câu 2 ạ mình cần gấp cảm ơn
Giúp mình làm câu 1 với ạ, mình đang cần gấp. Cảm ơn rất nhiều. 
\(\left(\dfrac{1}{2}+\dfrac{1}{3}\right)x\dfrac{5}{6}=\dfrac{5}{6}x\dfrac{5}{6}=\dfrac{25}{36}\)
Trả lời giúp mình câu phần 1 đọc hiểu với ạ, mình đang cần gấp
Mình cảm ơn!
Giải giúp mình gấp câu b, c với. Mình đang cần gấp. Mình cảm ơn.
b: Gọi giao của AH với BC là F
=>AH vuông góc BC tại F
góic CHI=góc AHD=90 độ-góc HAD=góc ABC=1/2*sđ cung AC
góc CIH=1/2*sđ cung CA
=>góc CHI=góc CIH
=>ΔCHI cân tại C
c:
góc BDC=góc BEC=90 độ
=>BDEC nội tiếp đường tròn đường kính BC
=>MD=ME
=>ΔMDE cân tại M
mà MN là trung tuyến
nên MN vuông góc DE
Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC
=>góc xAC=góc AED
=>Ax//DE
=>DE vuông góc OA
=>MN//AO
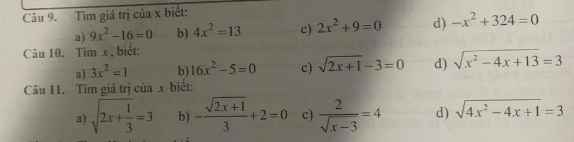
mình cần từ câu 9 đến 11 ạ mình cần gấp ạ cảm ơn
Câu 9:
a) Ta có: \(9x^2-16=0\)
\(\Leftrightarrow\left(3x-4\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
b) Ta có: \(4x^2=13\)
\(\Leftrightarrow x^2=\dfrac{13}{4}\)
\(\Leftrightarrow x\in\left\{\dfrac{\sqrt{13}}{2};-\dfrac{\sqrt{13}}{2}\right\}\)
c) Ta có: \(2x^2+9=0\)
\(\Leftrightarrow2x^2=-9\)(Vô lý)
d) Ta có: \(-x^2+324=0\)
\(\Leftrightarrow x^2=324\)
\(\Leftrightarrow\left[{}\begin{matrix}x=18\\x=-18\end{matrix}\right.\)
Giúp mình câu 5 với ạ. Mình cần gấp. Cảm ơn 
Câu 5:
a,C1:
còn câu b , thì mk chx đc hiểu cho lắm!
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
Giải gấp cho mình câu 2 với. Mình cần rất rất gấp. Cảm ơn rất nhiều.