Giúp mình với gấp lắm ạ
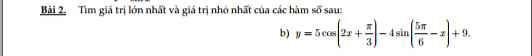
 giúp mình với ạ, mình cần gấp lắm ạ
giúp mình với ạ, mình cần gấp lắm ạ
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Giúp mình với ạ, mình cần gấp lắm ạ!
Lời giải:
Đặt \(\sqrt[3]{5\sqrt{2}+7}=m; \sqrt[3]{5\sqrt{2}-7}=n\)
\(m^3-n^3=14\)
\(mn=1\)
\((a+b+c)^3=(m-n)^3=m^3-3mn(m-n)-n^3=14-3(m-n)\)
\(\Leftrightarrow (a+b+c)^3=14-3(a+b+c)\)
\(\Leftrightarrow (a+b+c)^3+3(a+b+c)-14=0\)
\(\Leftrightarrow (a+b+c)^2[(a+b+c)-2]+2(a+b+c)(a+b+c-2)+7(a+b+c-2)=0\)
\(\Leftrightarrow (a+b+c-2)[(a+b+c)^2+2(a+b+c)+7]=0\)
Dễ thấy biểu thức trong ngoặc vuông $>0$ nên $a+b+c-2=0$
$\Leftrightarrow a+b+c=2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-1}{2}=\frac{3}{2}$
giúp mình với ạ mình cần gấp lắm ạ
5:
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc A chung
=>ΔABD đồng dạng với ΔACE
b; ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
c: ΔADE đồng dạng với ΔABC
=>S ADE/S ABC=(AD/AB)^2=1/4

mở bài là giới thiệu về cụ nha mn em viết lộn ạ
thân bài là đóng góp ạ
giúp mình với ạ, gấp lắm, mình đang ktra ạ

Giúp mình với ạ!! Gấp lắm ạ!!!
Giúp mình gấp với, gấp lắm ạ


Làm hết giúp mình với các bạn trình bày vẽ hình giúp mình với ạ gấp lắm ạ
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
 các bạn ơi giúp mình với ạ!!! mình cần gấp lắm ạ. mong các bạn giúp mình. cảm ơn ạ
các bạn ơi giúp mình với ạ!!! mình cần gấp lắm ạ. mong các bạn giúp mình. cảm ơn ạ ![]()
Giúp mình với mình gấp lắm ạ