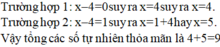Số các số tự nhiên thỏa mãn
là
NG
Những câu hỏi liên quan
số cásố các cặp số tự nhiên (x;y) thỏa mãn (x-y)(x+y)=2014 làc cặp số tự nhiên (x;y) thỏa mãn (x-y)(x+y)=2014 là...
a, có hay không ác số tự nhiên x, y thỏa mãn : (x+y)(x-y)=2014
b, có hay không các số tự nhiên x thỏa mãn x(x+1)(x+2)=2012
c, có hay không các số tự nhiên x, y thỏa mãn : (x+y)(x-y)=2011
d , có không các số tự nhiên x, y thỏa mãn : (x+y)(x-y)=2013
a, có hay không ác số tự nhiên x, y thỏa mãn : (x+y)(x-y)=2014
b, có hay không các số tự nhiên x thỏa mãn x(x+1)(x+2)=2012
c, có hay không các số tự nhiên x, y thỏa mãn : (x+y)(x-y)=2011
d , có không các số tự nhiên x, y thỏa mãn : (x+y)(x-y)=2013
:D :D :D :D
Viết các tập hợp sau rồi tìm số phần tử :
a) Tập hợp A các số tự nhiên X thỏa mãn : 7X . 7 = 0
b) Tập hợp B các số tự nhiên X thỏa mãn : 0 . X = 0
c) Tập hợp C các số tự nhiên X thỏa mãn : X + 2 = X - 2
DỄ LÉM ! AI NHANH MK TK CHO !
a) ta có: 7x7 = 0
49x = 0
=> x = 0
=> A = {0}
b) ta có: 0.x = 0
mà x là số tự nhiên
=> x thuộc N
=> B = { x thuộc N}
c) ta có: x + 2 = x - 2
=> x - x = - 2 - 2
\(\Rightarrow x\in\varnothing\)
\(\Rightarrow C=\left\{\varnothing\right\}\)
Đúng 1
Bình luận (0)
Tổng các số tự nhiên thỏa mãn x - 4 5 = x - 4 3 là
A. 8
B. 4
C. 5
D. 9
các bn giúp mình giải 1 số bài tập này nhé :
-tìm số tự nhiên n thỏa mãn :n+3 chia hết cho n-2
-tìm số tự nhiên n thỏa mãn :n+3 chia hết cho 2n -2
-tìm các số nguyên x thỏa mãn x lớn hơn hoặc bằng -21/7 và x bé hơn hoặc bằng 3
-tìm các số tự nhiên x,y thỏa mãn x-1 chia hết cho y , y-1 chia hết cho x
các số tự nhiên x thỏa mãn | x + 2 | = 10 là
x + 2 = 10 và -x - 2 = 10 \(⇔\) x= 8 và x = -12
Đúng 0
Bình luận (0)
Nhanh lên, không cần giải thích
Đúng 0
Bình luận (0)
x + 2 = 10 và -x - 2 = 10 \(\Leftrightarrow\) x= 8 và x = -12
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tập hợp các số tự nhiên x thỏa mãn 6 ⋮ (x - 2) là:
A. {1; 2; 3; 6}
B. {3; 6}
C. {5; 8}
D. {3; 4; 5; 8}
Đáp án là D
Vì 6 ⋮ (x - 2) ⇒ x - 2 ∈ U(6) = {1; 2; 3; 6}
• x - 2 = 1
x = 3
• x - 2 = 2
x = 4
• x - 2 = 3
x = 5
• x - 2 = 6
x = 8
Vậy x ∈ {3; 4; 5; 8}
Đúng 0
Bình luận (0)
Cho hai số tự nhiên x,y thỏa mãn: (x-3)(2y+5)=74. Tập hợp các giá trị y thỏa mãn là{...}
Tìm tất cả các số tự nhiên n thỏa mãn 9n2+3n+4 là số chính phương
Hôm nay olm.vn sẽ hướng dẫn các em cách giải phương trình nghiệm nguyên bằng nguyên lí kẹp. Cấu trúc đề thi hsg, thi chuyên thi violympic.
(3n + 1)2 = 9n2 + 2n + 1 < 9n2 + 3n + 4 \(\forall\) n \(\in\) N (1)
(3n + 2)2 = (3n + 2).(3n +2) = 9n2 + 12n + 4
⇒(3n + 2)2 ≥ 9n2 + 3n + 4 \(\forall\) n \(\in\) N (2)
Kết hợp (1) và (2) ta có: (3n +1)2 < 9n2 + 3n + 4 ≤ (3n + 2)2
Vì (3n + 1)2 và (3n +2)2 là hai số chính phương liên tiếp nên
9n2 + 3n + 4 là số chính phương khi và chỉ khi:
9n2 + 3n + 4 = (3n + 2)2 ⇒ 9n2 + 3n + 4 = 9n2 + 12n + 4
9n2 + 12n + 4 - 9n2 - 3n - 4 = 9n = 0 ⇒ n = 0
Vậy với n = 0 thì 9n2 + 3n + 4 là số chính phương.
Đúng 0
Bình luận (0)