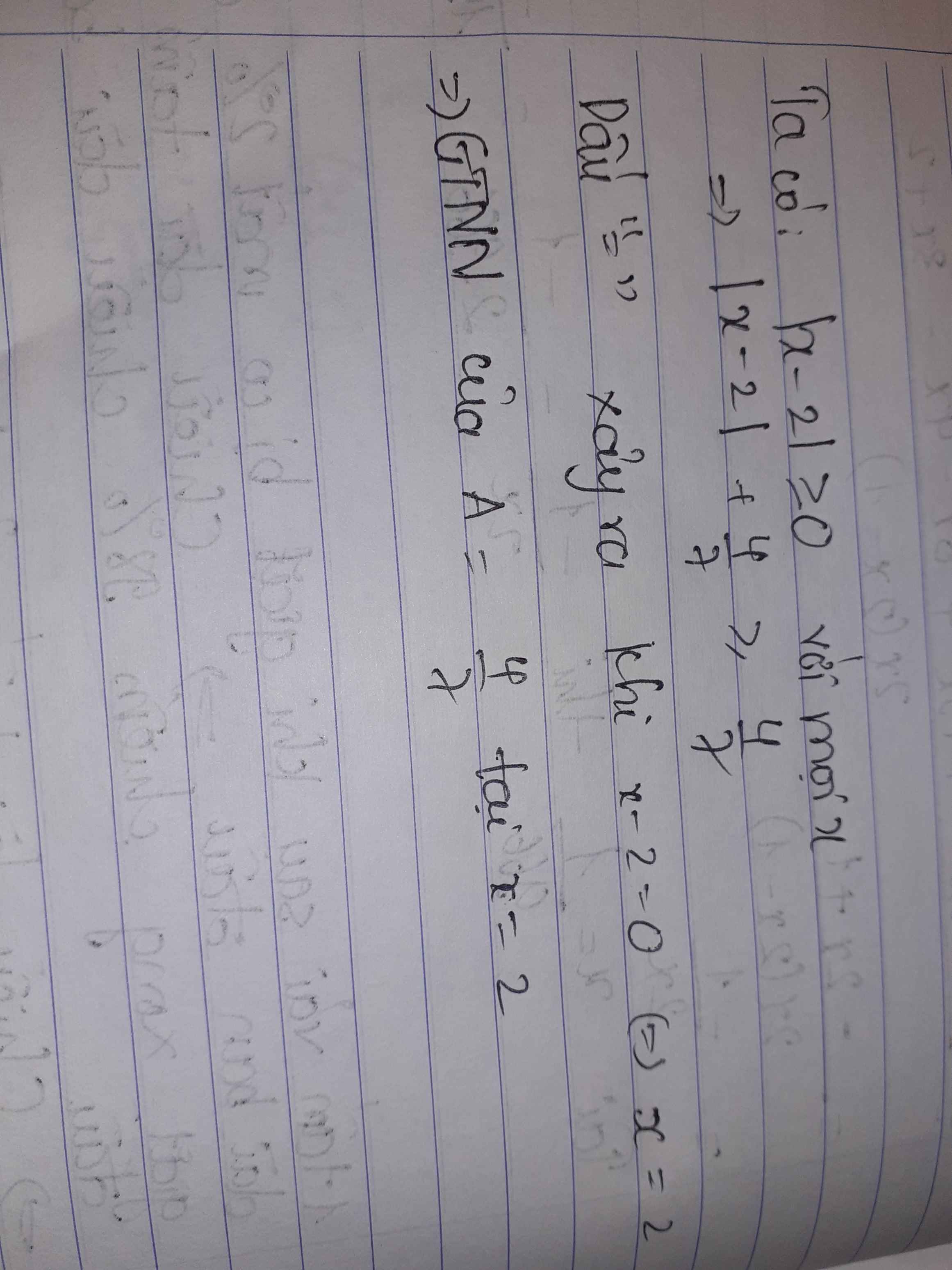Tìm giá trị nhỏ nhất của:A=(x+1)^4+|y-2|+3
TN
Những câu hỏi liên quan
1) Tìm giá trị nhỏ nhất của:
A= 2 . ( x - 3 )4 - 11
2) Tìm giá trị lớn nhất của :
B= -3 - |5-x|
(|: giá trị tuyệt đối)
1) `(x-3)^4 >=0`
`2.(x-3)^4>=0`
`2.(x-3)^4-11 >=-11`
`=> A_(min)=-11 <=> x-3=0<=>x=3`
2) `|5-x|>=0`
`-|5-x|<=0`
`-3-|5-x|<=-3`
`=> B_(max)=-3 <=>x=5`.
Đúng 1
Bình luận (0)
Bài 1:
Ta có: \(\left(x-3\right)^4\ge0\forall x\)
\(\Leftrightarrow2\left(x-3\right)^4\ge0\forall x\)
\(\Leftrightarrow2\left(x-3\right)^4-11\ge-11\forall x\)
Dấu '=' xảy ra khi x=3
Đúng 1
Bình luận (0)
Bài 2:
Ta có: \(\left|5-x\right|\ge0\forall x\)
\(\Leftrightarrow-\left|5-x\right|\le0\forall x\)
\(\Leftrightarrow-\left|5-x\right|-3\le-3\forall x\)
Dấu '=' xảy ra khi x=5
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của:
A= | x - 2 | + \(\dfrac{4}{7}\)
\(A=\left|x-2\right|+\dfrac{4}{7}\ge\dfrac{4}{7}\)
dấu"=" xảy ra \(< =>x=2\)
Đúng 2
Bình luận (1)
Ta có: \(\left|x-2\right|\ge0\forall x\)
\(\Leftrightarrow\left|x-2\right|+\dfrac{4}{7}\ge\dfrac{4}{7}\forall x\)
Dấu '=' xảy ra khi x-2=0
hay x=2
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của:A=/2.5-x/+5,8
Tìm giá trị lớn nhất của:B=2-/x+2/3/ (là 2 phần 3 nha mấy bạn)
ta có: /2,5-x/\(\ge\)0, nên A= /2,5-x/ + 5,8 \(\ge\)5,8
vậy giá trị nn của A là 5,8, A=5,8 khi /2,5-x/=0
<=> x=2,5
ta có: /x+2/3/ \(\ge\)0 nên B= 2 - /x+2/3/ \(\le\)2
vậy gtln của B là 2, B=2 khi /x+2/3/=0 <=> x= -2/3
Đúng 0
Bình luận (0)
Bài 1: Tìm giá trị nhỏ nhất của:a) A x2 + 2x + 4b) B x2 - 20x + 101c) C x2 - 2x + y2 + 4y + 8 Bài 2: Tìm giá trị lớn nhất của:A 5 - 8x - x2B x - x2C 4x - x2 + 3D -x2 + 6x - 11
Đọc tiếp
Bài 1: Tìm giá trị nhỏ nhất của:
a) A= x2 + 2x + 4
b) B= x2 - 20x + 101
c) C= x2 - 2x + y2 + 4y + 8
Bài 2: Tìm giá trị lớn nhất của:
A = 5 - 8x - x2
B = x - x2
C = 4x - x2 + 3
D = -x2 + 6x - 11
Bài 1:
a: \(A=x^2+2x+4\)
\(=x^2+2x+1+3\)
\(=\left(x+1\right)^2+3>=3\forall x\)
Dấu '=' xảy ra khi x+1=0
=>x=-1
Vậy: \(A_{min}=3\) khi x=-1
b: \(B=x^2-20x+101\)
\(=x^2-20x+100+1\)
\(=\left(x-10\right)^2+1>=1\forall x\)
Dấu '=' xảy ra khi x-10=0
=>x=10
Vậy: \(B_{min}=1\) khi x=10
c: \(C=x^2-2x+y^2+4y+8\)
\(=x^2-2x+1+y^2+4y+4+3\)
\(=\left(x-1\right)^2+\left(y+2\right)^2+3>=3\forall x\)
Dấu '=' xảy ra khi x-1=0 và y+2=0
=>x=1 và y=-2
Vậy: \(C_{min}=3\) khi (x,y)=(1;-2)
Bài 2:
a: \(A=5-8x-x^2\)
\(=-\left(x^2+8x\right)+5\)
\(=-\left(x^2+8x+16-16\right)+5\)
\(=-\left(x+4\right)^2+16+5=-\left(x+4\right)^2+21< =21\forall x\)
Dấu '=' xảy ra khi x+4=0
=>x=-4
b: \(B=x-x^2\)
\(=-\left(x^2-x\right)\)
\(=-\left(x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}< =\dfrac{1}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)
c: \(C=4x-x^2+3\)
\(=-x^2+4x-4+7\)
\(=-\left(x^2-4x+4\right)+7\)
\(=-\left(x-2\right)^2+7< =7\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
d: \(D=-x^2+6x-11\)
\(=-\left(x^2-6x+11\right)\)
\(=-\left(x^2-6x+9+2\right)\)
\(=-\left(x-3\right)^2-2< =-2\forall x\)
Dấu '=' xảy ra khi x-3=0
=>x=3
Đúng 4
Bình luận (0)
2) Tìm giá trị lớn nhất của:
A = 12 - (2,5 - y)^4 B = 10 - (3 + 4y)^2 - (x - 2y)^
\(A=12-\left(2,5-y\right)^4\le12\)
\(maxA=12\Leftrightarrow y=2,5\)
\(B=10-\left(3+4y\right)^2-\left(x-2y\right)^2\le10\)
\(maxB=10\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=-\dfrac{3}{4}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của:
A = \(\dfrac{27-12x}{x^2+9}\)
\(A=\dfrac{27-12x}{x^2+9}=\dfrac{x^2-12x+36-\left(x^2+9\right)}{x^2+9}=\dfrac{\left(x-6\right)^2}{x^2+9}-1\ge-1\)
\(A_{min}=-1\Leftrightarrow x=6\)
\(A=\dfrac{27-12x}{x^2+9}=\dfrac{4\left(x^2+9\right)-\left(4x^2+12x+9\right)}{x^2+9}=4-\dfrac{\left(2x+3\right)^2}{x^2+9}\le4\)
\(A_{max}=4\Leftrightarrow x=\dfrac{-3}{2}\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của:A=(x-2)^2+5; B=12+(3-x)^2
A = ( x - 2 ) ^ 2 + 5
=> A nhỏ nhất khi x = 2
Lúc đó giá trị của A = 5
B = 12 + ( 3 - x ) ^ 2
=> B nhỏ nhất khi x = 3
Lúc đó giá trị của B = 12
Đúng 0
Bình luận (0)
Tùm giá trị nhỏ nhất của:A=50+|x-5|+|y-3|
Ta có : \(\left|x-5\right|\ge0\forall x\)
\(\left|y-3\right|\ge0\forall y\)
\(\Rightarrow50+\left|x-5\right|+\left|y-3\right|\ge50\)
\(\Rightarrow\text{ Min A = 50}\)
Dấu "=" xảy ra khi
\(\hept{\begin{cases}\left|x-5\right|=0\\\left|y-3\right|=0\end{cases}\Rightarrow\hept{\begin{cases}x-5=0\\y-3=0\end{cases}\Rightarrow}\hept{\begin{cases}x=5\\y=3\end{cases}}}\)
Vậy GTNN của A = 50 khi \(\hept{\begin{cases}x=5\\y=3\end{cases}}\)
Đúng 0
Bình luận (0)
* Với giá trị nào của x thì các căn sau có nghĩa:
a.\(\sqrt{8x+2}\)
b.\(\sqrt{\dfrac{-5}{6-3x}}\)
* Tìm giá trị nhỏ nhất của:
A=\(x-2\sqrt{x-2}+3\)
$a)ĐK:8x+2\ge 0$
$\to 8x \ge -2$
$\to x \ge -\dfrac14$
$b)ĐK:\dfrac{-5}{6-3x} \ge 0(x \ne 2)$
Mà $-5<0$
$\to 6-3x<0$
$\to 6<3x$
$\to x>2$
$*A=x-2\sqrt{x-2}+3(x \ge 2)$
$=x-2-2\sqrt{x-2}+1+4$
$=(\sqrt{x-2}-1)^2+4 \ge 4$
Dấu "=" xảy ra khi $\sqrt{x-2}-1=0 \Leftrightarrow \sqrt{x-2}=1\Leftrightarrow x=3$
Đúng 0
Bình luận (0)
a) \(x\ge-\dfrac{1}{4}\)
b) x<2
Đúng 0
Bình luận (1)