Giúp mị và ập mị cảm ơn nhiều ạ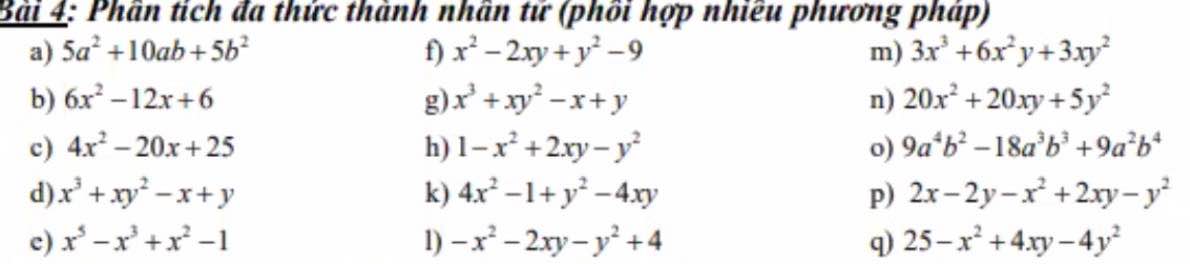
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
LL
Những câu hỏi liên quan
Giúp mũi làm bài tập và ập mị cảm ơn nhiều ạ
Hóa thân thành An Dương Vương kể lại Truyện An Dương Vương và Mị Châu, Trọng Thuỷ
Đừng chép mạng nha mọi người
Mình cảm ơn nhiều ạ
Giúp mik lm vs ập mik cảm ơn rất nhiều ạ 

Bài 17:
1) \(3^2-x^2=\left(3-x\right)\left(3+x\right)\)
2) \(x^2-36=\left(x-6\right)\left(x+6\right)\)
3) \(y^2-1=\left(y-1\right)\left(y+1\right)\)
4) \(25-y^2=\left(5-y\right)\left(5+y\right)\)
5) \(9x^2-1=\left(3x-1\right)\left(3x+1\right)\)
6) \(\dfrac{1}{25}-4x^2=\left(\dfrac{1}{5}-2x\right)\left(\dfrac{1}{5}+2x\right)\)
7) \(9x^2-y^2=\left(3x-y\right)\left(3x+y\right)\)
8) \(x^2-4y^2=\left(x-2y\right)\left(x+2y\right)\)
Đúng 2
Bình luận (1)
Bài 18:
1) \(\left(x-5\right)\left(x+5\right)=x^2-25\)
2) \(\left(4-x\right)\left(4+x\right)=16-x^2\)
3) \(\left(x-\dfrac{2}{3}\right)\left(x+\dfrac{2}{3}\right)=x^2-\dfrac{4}{9}\)
4) \(\left(1+2x\right)\left(1-2x\right)=1-4x^2\)
5) \(-\left(2x+3\right)\left(3-2x\right)=\left(2x+3\right)\left(2x-3\right)=4x^2-9\)
6) \(-\left(5x-3\right)\left(3+5x\right)=\left(3-5x\right)\left(3+5x\right)=9-25x^2\)
7) \(-\left(3x-\dfrac{2}{5}\right)\left(3x+\dfrac{2}{5}\right)=-\left(9x^2-\dfrac{4}{25}\right)=\dfrac{4}{25}-9x^2\)
8) \(-\left(2x-\dfrac{2}{3}\right)\left(2x+\dfrac{2}{3}\right)=-\left(4x^2-\dfrac{4}{9}\right)=\dfrac{4}{9}-4x^2\)
Đúng 1
Bình luận (1)
1)\(\left(x+2\right)^2\)
2)\(\left(x+3\right)^2\)
3)\(\left(2x+1\right)^2\)
4)\(\left(3+2x\right)^2\)
5)\(\left(x-1\right)^2\)
6)\(\left(x-4\right)^2\)
7)\(\left(6-x\right)^2\)
8)\(\left(2x-3y\right)^2\)
9)\(\left(3x-1\right)^2\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Giúp mình lm bài tập vs ập mình cảm ơn nhiều ạ 
<Lời khẩn cầu của Mị Châu trước khi chết có ý nghĩa gì?>
mk cần gấp các bn giúp mk vs mình cảm ơn nhiều:3
Tìm GTNN của \(A=\frac{2}{6x-5-9x^2}\)
Giúp mị nha -.- Mị cảm ơn trước !!!!!!
Ta có: A=\(\frac{-2}{9x^2-6x+1+4}\) =\(\frac{-2}{\left(3x-1\right)^2+4}\)\(\ge\)\(\frac{-2}{4}\)=\(\frac{-1}{2}\)
Vậy giá trị nhỏ nhất của A là \(\frac{-1}{2}\)khi x=\(\frac{1}{3}\)
Đúng 0
Bình luận (0)
\(A=\frac{2}{6x-5-9x^2}\)
\(A=\frac{2}{-9x^2+6x-1-4}\)
\(A=\frac{2}{-\left(9x^2-6x+1\right)-4}\)
\(A=\frac{2}{-\left(3x-1\right)^2-4}\)
Vì \(-\left(3x-1\right)^2\le0\)
\(\Rightarrow-\left(3x-1\right)^2-4\le-4\)
\(\Rightarrow\frac{2}{-\left(3x-1\right)^2-4}\ge\frac{2}{-4}\)
\(\Rightarrow A\ge\frac{-1}{2}\)
Vậy \(GTNN_A=\frac{-1}{2}\)tại \(x=\frac{1}{3}\)
Đúng 0
Bình luận (0)
\(A=\frac{2}{6x-5-9x^2}=\frac{-2}{9x^2-6x+5}=\frac{-2}{\left(3x-1\right)^2+4}\)
Ta thấy ( 3x - 1 )2 \(\ge0\)nên ( 3x - 1 )2 +4 \(\ge4\) do đó \(\frac{1}{\left(3x-1\right)^2+4}\le\frac{1}{4}\) theo t/c \(a\ge b\)thì \(\frac{1}{a}\le\frac{1}{b}\)( với a , b cùng dấu ) .
Do đó \(\frac{-2}{\left(3x-1\right)^2+4}\ge\frac{-2}{4}\Rightarrow A\ge-\frac{1}{2}\)
minA = \(-\frac{1}{2}\)<=> 3x - 1 = 0 <=> x = \(\frac{1}{3}\)
Đúng 0
Bình luận (0)
Cho biết A=-21 phần 102016+-12 phần 102017
B=-12 phần 102016+-21 phần 102017
So sánh A và B
Giúp mị nhanh nhanh nka mị cảm ơn
Cho tam giác ABC . Các tia phân giác của B và C cắt nhau tại I . CMR AI là tia phân giác của góc A ( vẽ hình hộ mình làm ơn hãy giúp mình , mình sẽ tick , 6:00 mình cần rồi , làm ơn giúp mị😢😢😢😢)
Cảm ơn rất nhiều !!! 😊😊
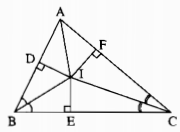
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
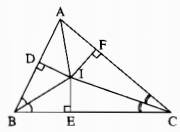
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W
Tính bằng cách hợp lí:
\(\left(1,11+0,19-2,6\right):\left(2,06+0,54\right)-\left(\frac{1}{2}+\frac{1}{3}\right):2\)
Giúp mị với , mị cảm ơn



