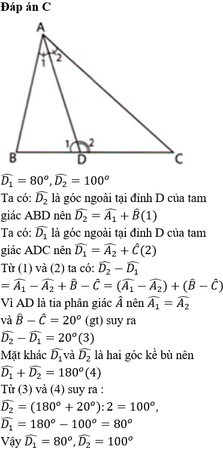
Cho tam giác ABC có B - C = 20o. Tia phân giác của góc A cắt BC ở D. Tính số đo các góc ADC và ADB.
LN
Những câu hỏi liên quan
Cc ho tam giáABC có: ∠B - ∠C = 20o. Tia phân giác của góc A cắt BC tại D. tính số đo các góc ∠(ADC) , ∠(ADB)
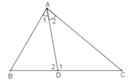
Trong ΔABD ta có ∠D1 là góc ngoài tại đỉnh D
∠D1 = ̂B + ∠A1 (tính chất góc ngoài của tam giác)
Trong ΔADC ta có ∠D2 là góc ngoài tại đỉnh D
∠D2 = ̂C + ∠A2 (tính chất góc ngoài của tam giác)
Ta có: ∠B > ∠C (gt); ∠A1 = ∠A2 (gt)
⇒∠D1 - ∠D2 = (B + ∠A1) - (C + ∠A2) = ∠B - ∠C = 20o
Lại có: ∠D1 + ∠D2 = 180o (hai góc kề bù)
⇒∠D1 = (180o + 20o):2 = 100o
⇒∠D1 = (100o - 20o) = 80o
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B - C = 20 độ. Tia phân giác của góc A cắt Bc ở D. Tính số đo các góc ADC, ADB
Đặt \(\widehat{ADC}=b;\widehat{ADB}=a\)
Ta có: \(a+\widehat{B}+\widehat{BAD}=b+\widehat{C}+\widehat{CAD}\)
\(\Leftrightarrow a+\widehat{C}+20^0=b+\widehat{C}\)
\(\Leftrightarrow a-b=-20\)
mà a+b=180
nên 2a=160
=>a=80
=>b=100
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B - góc C = 20 độ . Tia phân giác của góc A cắt BC ở D . Tính số đo góc ADC và ADB
Cho tam giác ABC có góc B - góc C =20o. Tia phân giác của góc A cắt BC ở D. Tính Số đo các góc ADC, góc ADB
Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo
A
D
C
^
biết
B
^
-
C
^
20
o
A. 80
°
B. 110
°
C. 100
°
D. 105
°
Đọc tiếp
Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo A D C ^ biết B ^ - C ^ = 20 o
A. 80 °
B. 110 °
C. 100 °
D. 105 °
Cho tam giác ABC có góc B - góc C =20o. Tia phân giác của góc A cắt BC ở D. Tính Số đo các góc ADC, góc ADB
cho tam giác ABC có góc B = 80 độ, góc C = 44 độ. Tia phân giác của góc A cắt BC ở D. Tính số đo của góc : A, ADB,ADC
Cho tam giác ABC có B-C =20 độ. Tia phân giác của góc A cắt BC ở D . Tính số đo góc ADC, góc ADB
Cho tam giác ABC có B - C = 180 . Tia phân giác góc A cắt BC tại D . Tính số đo góc ADC ? góc ADB ?
Xét tam giác ABC: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\Rightarrow\widehat{B}+\widehat{C}=180^0-\widehat{A}\)
Mặt khác: \(\widehat{B}-\widehat{C}=18^0\Rightarrow\left\{{}\begin{matrix}\widehat{B}=\dfrac{180^0-\widehat{A}+18^0}{2}=99^0-\dfrac{\widehat{A}}{2}\\\widehat{C}=99^0+\dfrac{\widehat{A}}{2}-18^0=81^0-\dfrac{\widehat{A}}{2}\end{matrix}\right.\)
Xét tam giác ABD: \(\widehat{ADC}=\widehat{BAD}+\widehat{B}=\dfrac{\widehat{A}}{2}+99^0-\dfrac{\widehat{A}}{2}=99^0\)
\(\widehat{ABD}=180^0-\widehat{ADC}=81^0\)
Đúng 0
Bình luận (0)