Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
x^2<9
giải bất phương trình và biểu diễn tập nghiệm trên trục số:x(x-1)-3(x-2)<x^2-4(x+2)
giải bất phương trình và biểu diễn tập hợp ngiệm trên trục số:
X-8>=2(x+1/2)+7
\(x-8\ge2\left(\dfrac{x+1}{2}\right)+7\)
⇔\(x-8\ge x+1+7\)
⇔\(x-x\ge1+7+8\)
⇔\(0x\ge16\)(vô lí)
Tập nghiệm của bất phương trình là :
\(S=\left\{\varnothing\right\}\)
\(x-8\ge2\left(x+\dfrac{1}{2}\right)+7\)
\(\Leftrightarrow x-8\ge2x+1+7\)
\(\Leftrightarrow-x\ge16\Leftrightarrow x\le-16\)
tập nghiệm của phương trình: S={ x | x \(\le-16\) }
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số: a, 3x -11 >5 -x
\(a,3x-11>5-x\\ \Leftrightarrow3x+x>5+11\\ \Leftrightarrow4x< 16\\ \Leftrightarrow x>4\)
Vậy bất phương trình có nghiệm là: \(S=\left\{x|x>4\right\}\)
biểu diễn
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số
a) 2x - 1 ≥ 5
b) x-2 /3 ≥ x - x-1 /2
a: 2x-1>=5
nên 2x>=6
hay x>=3
b: \(\dfrac{x-2}{3}>=x-\dfrac{x-1}{2}\)
=>2x-4>=6x-3(x-1)
=>2x-4>=6x-3x+3
=>2x-4>=3x+3
=>-x>=7
hay x<=-7
a.\(2x-1\ge5\)
\(\Leftrightarrow2x\ge6\)
\(\Leftrightarrow x\ge3\)
Vậy \(S=\left\{x|x\ge3\right\}\)
b.\(\dfrac{x-2}{3}\ge x-\dfrac{x-1}{2}\)
\(\Leftrightarrow\dfrac{2\left(x-2\right)}{6}\ge\dfrac{6x-3\left(x-1\right)}{6}\)
\(\Leftrightarrow2\left(x-2\right)\ge6x-3\left(x-1\right)\)
\(\Leftrightarrow2x-4\ge6x-3x+3\)
\(\Leftrightarrow-x\ge7\)
\(\Leftrightarrow x\le7\)
Vậy \(S=\left\{x|x\le7\right\}\)
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
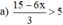
⇔ 15 – 6x > 15 (Nhân cả hai vế với 3 > 0, BPT không đổi chiều)
⇔ -6x > 15 – 15 (Chuyển vế và đổi dấu hạng tử 15)
⇔ -6x > 0
⇔ x < 0 (Chia cả hai vế với -6 < 0, BPT đổi chiều)
Vậy nghiệm của bất phương trình là x < 0.

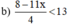
⇔ 8 – 11x < 13.4 (Nhân cả hai vế với 4 > 0, BPT không đổi chiều)
⇔ 8 – 11x < 52
⇔ -11x < 52 – 8 (Chuyển vế và đổi dấu hạng tử 8)
⇔ -11x < 44
⇔ x > 44 : (-11) (Chia cả hai vế cho -11 < 0, BPT đổi chiều
⇔ x > -4.
Vậy bất phương trình có nghiệm x > -4.

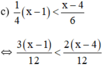
⇔ 3(x – 1) < 2(x – 4) (Nhân cả hai vế với 12 > 0, BPT không đổi chiều)
⇔ 3x – 3 < 2x – 8
⇔ 3x – 2x < -8 + 3 (Chuyển vế và đổi dấu 2x và -3)
⇔ x < -5
Vậy bất phương trình có tập nghiệm x < -5.

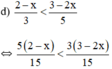
⇔ 5(2 – x) < 3(3 – 2x) (Nhân cả hai vế với 15 > 0, BPT không đổi chiều)
⇔ 10 – 5x < 9 – 6x
⇔ 6x – 5x < 9 – 10 (Chuyển vế và đổi dấu -6x và 10)
⇔ x < -1.
Vậy bất phương trình có tập nghiệm x < -1.

giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số
a) 2x-8≥≥0.
b)10+10x>0
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 2 3 x − 9 > x + 1 3 ; b) 4 x 3 x + 2 − 7 ≤ 3 2 x − 1 2
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số
d) 3 - 2x ≤ 4
e) 5x - 2 ≤ 2x + 8
f) 2(x - 3) + 12 ≤ x + 2
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số
d) 3 - 2x ≤ 4
e) 5x - 2 ≤ 2x + 8
f) 2(x - 3) + 12 ≤ x + 2
d: =>-2x<=1
=>x>=-1/2
e: =>3x<=10
=>x<=10/3
f: =>2x-6+12<=x+2
=>2x+6<=x+2
=>x<=-4