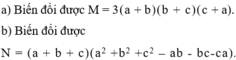Phân tích đa thức thành nhân tử:
a) 45a3-30a2+5a-500
b) a2b-49b+14b2-b3
H24
Những câu hỏi liên quan
Phân tích đa thức thành nhân tử:
a) 7a3-28a2+28a
b) 45a3-30a2+5a-500
c) a2b-49b+14b2-b3
d) x4+4
a) $7a^3 - 28a^2 + 28a$
$ = 7a.(a^2 - 4a+4)$
$ = 7a.(a-2)^2$
d) $x^4 + 4$
$ = (x^4+4x^2+4) - 4x^2$
$ = (x^2+2)^2 - (2x)^2$
$ = (x^2+2x+2)(x^2-2x+2)$
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử:
a) 10x3-90x5
b) 3a2-6a2b+5a-10ab
c) 7a3-28a2+28a
d) 45a3-30a2+5a-500
e) a2b-49b+14b2-b3
f) x4+4
Phân tích đa thức thành nhân tử:
a) 10x3-90x5
b) 3a2-6a2b+5a-10ab
c) 7a3-28a2+28a
d) 45a3-30a2+5a-500
e) a2b-49b+14b2-b3
f) x4+4
a) 10x3-90x5=10x3(1-9x2)=10x3(1-3x)(1+3x)
b)3a2-6a2b+5a-10ab=(3a2-6a2b)+(5a-10ab)=3a2(1-2b)+5a(1-b)=(3a2+5a)(1-2b)=a(3a+5)(1-2b)
c) 7a3-28a2+28a=7a(a2-4a+4)
d) 45a3-30a2+5a-500=5(9a3-6a2+a-100)
Đúng 1
Bình luận (0)
phân tích đa thức thành nhân tử: a2b+a2c+ab2+ac2+c2b+cb2+2abc
Phân tích đa thức
a
4
+
a
3
+
a
3
b
+
a
2
b
thành nhân tử bằng phương pháp nhóm hạng tử A.
a
2
a
+
b
a
+
1...
Đọc tiếp
Phân tích đa thức a 4 + a 3 + a 3 b + a 2 b thành nhân tử bằng phương pháp nhóm hạng tử
A. a 2 a + b a + 1
B. a a + b a + 1
C. a 2 + a b a + 1
D. a + b a + 1
Ta có
a 4 + a 3 + a 3 b + a 2 b = a 4 + a 3 + a 3 b + a 2 b = a 3 a + 1 + a 2 b a + 1 = a + 1 a 3 + a 2 b = a + 1 a 2 a + b = a 2 a + b a + 1
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử a(b3-c3)+b(c3-a3)+c(a3-b3)
a(b3 - c3) + b(c3 - a3) + c(a3 - b3)
= a(b3 - c3 ) + b( c3 - b3 + b3 - a3) + c(a3 - b3)
= a(b3 - c3) + b(c3 - b3) + b(b3 - a3) + c(a3 - b3)
= a(b3 - c3) - b(b3 - c3) - [b(a3 - b3) - c(a3- b3)]
= (b3 - c3)(a - b) - (a3- b3)(b - c)
= (b - c)(b2 + bc + c2)(a - b) - (a - b)(a2 + ab + b2)(b - c)
= (b - c)(a - b)(b2 + bc + c2 - a2 + ab - b2)
= (b - c)(a - b) [ (c2 - a2) + (bc - ab) ]
= (b - c)(a - b) [ (c - a)(c + a) + b(c - a) ]
= (b - c)(a -b) [ (c - a)(c + a + b) ]
= (a- b)(b - c)(c - a)(a + b + c)
Phân tích đa thức thành nhân tử:a) M
(
a
+
b
+
c
)
3
-
a
3
-
b
3
-
c...
Đọc tiếp
Phân tích đa thức thành nhân tử:
a) M = ( a + b + c ) 3 - a 3 - b 3 - c 3 ;
b) N = a 3 + b 3 + c 3 - 3abc.
5a(a-2)(a+2)
phân tích đa thức thành nhân tử
Bạn xem lại đề bài nhé.
Đúng 1
Bình luận (1)
phân tích đa thức thành nhân tử: 9a2b+6ab2+b3-6ab-2b
\(9a^2b+6ab^2+b^3-6ab-2b^2\)
\(=b\left(9a^2+6ab+b^2-6a-2b\right)\)
\(=b\left[\left(3a+b\right)^2-2\left(3a+b\right)\right]\)
\(=b\left(3a+b\right)\left(3a+b-2\right)\)
Đúng 0
Bình luận (0)