Cho tam giác ABC vuông tại A,biết góc B60 độ,BC=10cm.Tính độ dài cạnh AB
MC
Những câu hỏi liên quan
cho Tam giác ABC vuông tại A, biết AB=6cm, BC=10cm.Tính độ dài cạnh AC và chu vi tam giác ABC
AC=AB.AB+BC.BC
=6.6+10.10
=36+100
=136
=11.6
Chu vi tam giác= AB=AC=BC=6+10+11=27
(Ko biết có làm đúng ko)
Đúng 0
Bình luận (0)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=10^2-6^2=64\)
hay AC=8(cm)
Vậy: AC=8cm
Chu vi của tam giác ABC là:
C=AB+AC+BC=6+8+10=24(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại B, đường phân giác góc C cắt AB tại D, đường thẳng kẻ từ A vuông góc với CD kéo dài tại H.
A.Cm tam giác HAD và tam giác BCD đồng dạng
B.Cm AH^2=HD.HC
C.Cho biết AB=6cm,AC=10cm.Tính độ dài đoạn thẳng BC và AD
a: Xét ΔHAD vuông tại H và ΔBCD vuông tại B có
\(\widehat{HDA}=\widehat{BDC}\)
Do đó; ΔHAD~ΔBCD
b: ta có; ΔHAD~ΔBCD
=>\(\widehat{BCD}=\widehat{HAD}\)
mà \(\widehat{BCD}=\widehat{ACD}\)
nên \(\widehat{HAD}=\widehat{ACD}\)
Xét ΔHAD vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAD}=\widehat{HCA}\)
Do đó: ΔHAD~ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HD}{HA}\)
=>\(HA^2=HD\cdot HC\)
c: Ta có: ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC^2=10^2-6^2=64\)
=>\(BC=\sqrt{64}=8\left(cm\right)\)
Xét ΔCBA có CD là phân giác
nên \(\dfrac{BD}{BC}=\dfrac{DA}{CA}\)
=>\(\dfrac{BD}{8}=\dfrac{DA}{10}\)
=>\(\dfrac{BD}{4}=\dfrac{DA}{5}\)
mà BD+DA=BA=6cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{4}=\dfrac{DA}{5}=\dfrac{BD+DA}{4+5}=\dfrac{6}{9}=\dfrac{2}{3}\)
=>\(DA=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông góc tại A có độ dài cạnh AB là 30 m,độ dài cạnh AC là 40 m ,độ dài cạnh BC là 50 m.Từ A hạ đường vuông góc AH xuống BC ,biết HC =38M.
a.Tính dt các tam giác :ABC;ABH;AHC.
B.Từ H hạ các đường vuông góc HD ,HE xuống AB ,AC.Tính dt hcn ADHE
Cho tam giác ABC vuông tại A, biết góc B=60 độ, BC=10cm. Tính độ dài cạnh AB
con này ngu bỏ mẹ có làm nó cũng k biết đúng,sai
ngu j làm cho hại não với những đứa ngu
Đúng 0
Bình luận (2)
vì trong tam giác vuông cạnh đối diện với góc 30 độ thì bằng 1nửa cạnh huyền nên AB =1/2 BC
\(\Rightarrow\)AB =5 cm
Đúng 0
Bình luận (0)
Bài 7: a, Cho tam giác ABC vuông tại A có AB 3 AC 4 = và BC = 5. Tính độ dài AB, AC b, Tính độ dài cạnh huyền biết độ dài hai cạnh góc vuông là 6 và 7 c, Tính góc ở đỉnh của tam giác cân biết số đo góc ở đáy là 200 d, Tính số đo góc ở đáy tam giác cân biết số đo góc ở đỉnh là 600
b: Độ dài cạnh huyền là \(\sqrt{6^2+7^2}=\sqrt{85}\left(cm\right)\)
c: Số đo góc ở đỉnh là:
\(180-2\cdot20^0=140^0\)
d: Số đó góc ở đáy là:
\(\dfrac{180^0-60^0}{2}=60^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB trên AC = 3 phần 4
và BC =100cm.
a) Tính độ dài AB AC , .
b) Tính độ dài hình chiếu của các cạnh góc vuông tam giác ABC trên cạnh BC
Cho tam giác ABC vuông tại A có BC= 12cm. Tính độ dài 2 cạnh góc vuông biết AB=3/2AC
Áp dụng định lý pytago có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\left(\dfrac{3}{2}AC\right)^2+AC^2=12^2\)
\(\Leftrightarrow AC=\dfrac{24\sqrt{13}}{13}\) cm
Suy ra \(AB=\dfrac{36\sqrt{13}}{13}\) cm
Vậy...
Đúng 1
Bình luận (0)
Tam giác ABC vuông tại A có AB = 6cm,AC =8cm, BC=10cm.Tính độ dài chiều cao AH
hình tự vẽ
xét tam giá ABC vuông tại A, đường cao AH
=> AB.AC=BC.AH(hệ thức lượng)
=>AH=(AB.AC)/BC=4,8(cm)
vậy AH= 4,8 cm
Đúng 0
Bình luận (0)
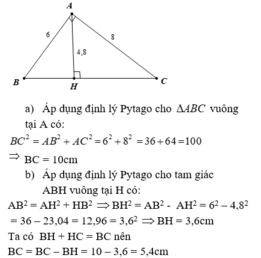
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. a) Tính độ dài cạnh BC. b)Kẻ AH vuông góc BC. Biết AH = 4,8cm. Tính độ dài các đoạn BH, CH .