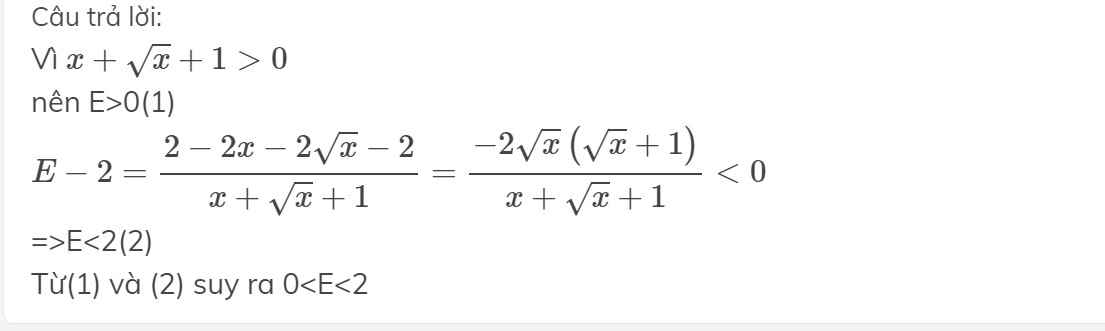Cho E={0;1;2;3;4;5;6} . có thể tạo được bao nhiêu số tự nhiên gồm 6 chữ số khác nhau lớn hơn 250000
HT
Những câu hỏi liên quan
cho m,n,e khác 0 và m+n+e=0 tính G=(1+m/n)*(1+n/e)*(1+e/m)
M={ x E N / m - x = 5}
N={ x E N / x . 0= 0}
O={ x E n / 0.x= 0}
P={ x E n / x chia het cho 4 va x < 100 }
Q={ x En / x = 2n; x <100; n E N*}
R={ x En/ x + 9 = 7
Luu y E la` Thuoc nha!!
CHO E HỎI MẸ E MUA CHO E CUỐN SÁCH GIÁ 139.984Đ CÔ CỬA HÀNG BỚT GIÁ CHO MẸ E CÒN 138.500Đ VẬY MẸ E ĐƯỢC CHIẾC KHẤU NHIÊU PHẦN TRĂM Ạ?
giá tiền được chiết khấu của quyển sách là :
\(139.984-138.500=1.484Đ\)
Phần trăm chiết khấu là : \(\frac{1.484}{139.984}\times100\%=1.06\%\)
Cho x thuộc Z và E=(1-x)4.(-x).Với điều kiện nào của x thì E = 0 :; E < o; E>0
( Trình bày đầy đủ hộ em với ạ )
a, Cho x e Q , x = a-5 / a ( a khác 0 ) với giá trị nguyên của a thì x e z
b, Cho x = a- 3 / 2a ( a khác 0 ) Với mọi giá trị nguyên của a thì x e z
x>0 y>0 x+y=4
tìm min E cho x>0 y>0 và x+y=4 tìm min E= (x+1/x)^2 +(y+1/y)^2 +2018
Đếm Số Phần Tử Của Các Tập Hợp Sau:
A={x E N/1000 chia hết cho x;10<x<50}
B={x E N/(x-5) . (x-4)=0}
C={x E N/x.(x+1)=0}
D={x E N/(x+13) .(x+10)=0}
![]()
Đúng 0
Bình luận (0)
Cho elip (E) có các tiêu điểm
F
1
-
5
;
0
,
F
2
5
;
0
và một điểm M nằm trên (E) sao cho chu vi của tam giác
M
F
1
F
2
bằng 30. Khi đó phương trình chính tắc của elip là: A. ...
Đọc tiếp
Cho elip (E) có các tiêu điểm F 1 - 5 ; 0 , F 2 5 ; 0 và một điểm M nằm trên (E) sao cho chu vi của tam giác M F 1 F 2 bằng 30. Khi đó phương trình chính tắc của elip là:
A. x 2 75 + y 2 100 = 1
B. 100 x 2 + 75 y 2 = 1
C. 75 x 2 + 100 y 2 = 1
D. x 2 100 + y 2 75 = 1
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho bt E= 2/( x +√x +1). CMR: 0<E<2