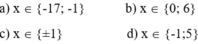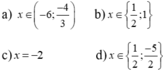giải phương trình : |x-2|+|x+1|+x3-5=0
H24
Những câu hỏi liên quan
Giải các phương trình sau:
i, (2x-1)2+(2-x)(2x-1)=0 j, (x-1)(5x+3)=(3x-5)(x-1) k, (4x+20)(x-6)=0 m, x3+x2+x+1=0 |
i,<=>(2x - 1)(2x - 1 + 2 - x) = 0 <=> (2x - 1)(x + 1) = 0
<=> x = 1/2 hoặc x = -1
j,<=>(x - 1)(5x + 3) - (3x - 5)(x - 1) = 0
<=>(x - 1)(2x + 8) = 0 <=> x = 1 hoặc x = -4
k,<=>4(x + 5)(x - 6) = 0 <=> (x + 5)(x - 6) = 0
<=> x = -5 hoặc x = 6
m,<=>x^2(x + 1) + x + 1 = 0
<=>(x^2 + 1)(x + 1) = 0 (1)
Mà x^2 + 1 > 0 với mọi x nên (1) xảy ra <=> x + 1 = 0
<=> x = -1
Đúng 1
Bình luận (0)
Bài 5: Tìm x (Giải phương trinh)
a)x^3-13x=0
b) 5x(x – 2000) – x + 2000 = 0
c) 2x(x – 2) + 3(x – 2) = 0
d) x + 1 = (x + 1)2
e) x + 5x2 = 0
f) x3 + x = 0
Bài 5: Tìm x (Giải phương trình)
a)x^3-13x=0 b) 5x(x – 2000) – x + 2000 = 0
c) 2x(x – 2) + 3(x – 2) = 0 d) x + 5x2 = 0
d) x + 1 = (x + 1)2 e) x3 + x = 0
b) 5x(x-2000)-x+2000=0
\(\Rightarrow5x\left(x-2000\right)-\left(x-2000\right)=0\\ \Rightarrow\left(x-2000\right)\left(5x-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x-2000=0\\5x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0+2000\\5x=0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\5x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\x=\dfrac{1}{5}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Ai giúp minh làm bài 5 phía trên với
Đúng 0
Bình luận (0)
c) Ta có: \(2x\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-3}{2}\end{matrix}\right.\)
d) Ta có: \(5x^2+x=0\)
\(\Leftrightarrow x\left(5x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-1}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài 5: Giải các phương trình sau:a. (3x - 1)2 - (x + 3)2 0b. x3 dfrac{x}{49}c. x2 - 7x + 12 0d. 4x2 - 3x -1 0e. x3 - 2x - 4 0f. x3 + 8x2 + 17x +10 0g. x3 + 3x2 + 6x + 4 0h. x3 - 11x2 + 30x 0
Đọc tiếp
Bài 5: Giải các phương trình sau:
a. (3x - 1)2 - (x + 3)2 = 0
b. x3 = \(\dfrac{x}{49}\)
c. x2 - 7x + 12 = 0
d. 4x2 - 3x -1 = 0
e. x3 - 2x - 4 = 0
f. x3 + 8x2 + 17x +10 = 0
g. x3 + 3x2 + 6x + 4 = 0
h. x3 - 11x2 + 30x = 0
a. (3x - 1)2 - (x + 3)2 = 0
\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)
\(\Leftrightarrow4x+2=0\) hoặc \(2x-4=0\)
1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)
2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)
S=\(\left\{-\dfrac{1}{2};2\right\}\)
Đúng 3
Bình luận (0)
b. \(x^3=\dfrac{x}{49}\)
\(\Leftrightarrow49x^3=x\)
\(\Leftrightarrow49x^3-x=0\)
\(\Leftrightarrow x\left(49x^2-1\right)=0\)
\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(7x+1=0\) hoặc \(7x-1=0\)
1. x=0
2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)
3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)
Đúng 2
Bình luận (0)
*Cách khác:
a) Ta có: \(\left(3x-1\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(3x-1\right)^2=\left(x+3\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=-x-3\\3x-1=x+3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=-2\\2x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=2\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{1}{2};2\right\}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình: (x – 1)(x2 + 3x – 2) – (x3 – 1) = 0.
(x – 1)(x2 + 3x – 2) – (x3 – 1) = 0
⇔ (x – 1)(x2 + 3x - 2) - (x - 1)(x2 + x + 1) = 0
⇔ (x – 1)[(x2 + 3x - 2) - (x2 + x + 1)] = 0
⇔ (x – 1). (x2 + 3x - 2 - x2 - x - 1) = 0
⇔ (x – 1)(2x - 3) = 0
⇔ x - 1 = 0 hoặc 2x - 3 = 0
+) Nếu x - 1 = 0 ⇔x = 1
+) Nếu 2x - 3 = 0 ⇔x = 3/2
Vậy tập nghiệm của phương trình là S = {1;3/2}
Đúng 0
Bình luận (0)
Giải các phương trình sau bằng cách đưa về phương trình tích x 3 – 5 x 2 –x +5 = 0
Ta có: x 3 – 5 x 2 –x +5 = 0 ⇔ x 2 ( x -5) – ( x -5) =0
⇔ (x -5)(x2 -1) =0 ⇔ (x -5)(x -1)(x +1) =0
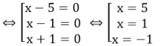
Vậy phương trình đã cho có 3 nghiệm :x1 = 5;x2 =1;x3=-1
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
7
−
x
2
4
−
x
+
5
2
0
;
b)
4
x
2
+
x
−
1...
Đọc tiếp
Giải các phương trình sau:
a) 7 − x 2 4 − x + 5 2 = 0 ;
b) 4 x 2 + x − 1 2 − 2 x + 1 2 = 0 ;
c) x 3 + 1 = x + 1 2 − x ;
d) x 2 − 4 x − 5 = 0 .
Giải các phương trình sau: (x – 1)( x 2 + 5x – 2) – ( x 3 – 1) = 0
(x – 1)( x 2 + 5x – 2) – ( x 3 – 1) = 0
⇔ (x – 1)( x 2 + 5x – 2) – (x – 1)( x 2 + x + 1) = 0
⇔ (x – 1)[( x 2 + 5x – 2) – ( x 2 + x + 1)] = 0
⇔ (x – 1)( x 2 + 5x – 2 – x 2 – x – 1) = 0
⇔ (x – 1)(4x – 3) = 0 ⇔ x – 1 = 0 hoặc 4x – 3 = 0
x – 1 = 0 ⇔ x = 1
4x – 3 = 0 ⇔ x = 0,75
Vậy phương trình có nghiệm x = 1 hoặc x = 0,75
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
x
−
1
2
−
2
x
+
5
2
0
;
b)
x
2
−
1
−
x
2...
Đọc tiếp
Giải các phương trình sau:
a) x − 1 2 − 2 x + 5 2 = 0 ;
b) x 2 − 1 − x 2 − 2 x − 1 2 = 0 ;
c) x 3 + 8 = − 2 x x + 2 ;
d) 4 x 2 + 8 x − 5 = 0 .
giải phương trình sau:a,x2(x+4,5)13,5;b) 4(x+1)2-9(x-1)2 0;c) (x-1)3+x3+ (x + 1)3 (x + 2)3.
Đọc tiếp
giải phương trình sau:
a,x2(x+4,5)=13,5;
b) 4(x+1)2-9(x-1)2= 0;
c) (x-1)3+x3+ (x + 1)3 = (x + 2)3.
b: 4(x+1)^2-9(x-1)^2=0
=>(2x+2)^2-(3x-3)^2=0
=>(2x+2-3x+3)(2x+2+3x-3)=0
=>(-x+5)(5x-1)=0
=>x=1/5 hoặc x=5
c: (x-1)^3+x^3+(x+1)^3=(x+2)^3
=>x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1=x^3+6x^2+12x+8
=>3x^3+6x-x^3-6x^2-12x-8=0
=>2x^3-6x^2-6x-8=0
=>x^3-3x^2-3x-4=0
=>x^3-4x^2+x^2-4x+x-4=0
=>(x-4)(x^2+x+1)=0
=>x-4=0
=>x=4
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
x
+
3
3
−
x
−
1
3
0
;
b)
x
4
+
x
2
−
2
0
;
c)
x
3...
Đọc tiếp
Giải các phương trình sau:
a) x + 3 3 − x − 1 3 = 0 ;
b) x 4 + x 2 − 2 = 0 ;
c) x 3 + 3 x 2 + 6 x + 4 = 0 ;
d) x 3 − 6 x 2 + 8 x = 0 .
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được ![]()
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
Đúng 0
Bình luận (0)