Bài 4:

\(A=2x^2-15\ge-15\\ A_{min}=-15\Leftrightarrow x=0\\ B=2\left(x+1\right)^2-17\ge-17\\ B_{min}=-17\Leftrightarrow x=-1\)

Bài 5:

\(A=-x^2+14\le14\\ A_{max}=14\Leftrightarrow x=0\\ B=25-\left(x-2\right)^2\le25\\ B_{max}=25\Leftrightarrow x=2\)

Ta có : \(B=14+2x-2x^2\)

\(\Rightarrow2B=2.\left(-2x^2+2x+14\right)\)

\(\Rightarrow2B=-4x^2+4x+28\)

\(\Rightarrow2B=-\left(2x\right)^2+2.2x-1+29\)

\(\Rightarrow2B=\left[\left(2x\right)^2-2.2x+1\right]+29\)

\(\Rightarrow2B=-\left(2x+1\right)^2+29\le29\)

\(\Rightarrow B\le\frac{29}{2}\)

Đẳng thức xảy ra khi : \(2x-1=0\Rightarrow x=\frac{1}{2}\)

Vậy \(B_{MAX}=\frac{29}{2}\) khi \(x=\frac{1}{2}\)

Ta có : \(B=14+2x-2x\\ =>2B=2\left(-x^2+2x+14\right)\\ =>2B=-4^2+4x+28\\ =>2B=-\left(2x\right)^2+2.2x-1+29\\ \)

\(=>2B=\text{[(2x)^2-2.2x+1]+29=>2B=-(2x+1)^2+29\le}29\\ =>B\le\frac{29}{2}\)

Đẳng thức xảy ra khi : \(2x-1=0=>x=\frac{1}{2}\\ V\text{ậy}B_{M\text{AX}}=\frac{29}{2}khix=\frac{1}{2}\)

Ta có: B = 14 + 2x - 2x²  => 2B = 2 . ( -2x² + 2x + 14 )  => 2B = -4x² + 4x + 28  => 2B = - (2x)² + 2 . 2x - 1 + 29     => 2B = - [ (2x)² - 2 . 2x + 1 ] + 29

=> 2B =  - (2x + 1)² + 29 \(\le\)29         =>  B \(\le\frac{29}{2}\)

Đẳng thức xảy ra khi: 2x - 1 = 0  => x = \(\frac{1}{2}\)

Vậy giá trị lớn nhất của B = \(\frac{29}{2}\)khi x = \(\frac{1}{2}\)

Lời giải:
Ta thấy:

$2x^2+2x+5=2(x^2+x+\frac{1}{4})+\frac{9}{2}$

$=2(x+\frac{1}{2})^2+\frac{9}{2}\geq 0+\frac{9}{2}=\frac{9}{2}$

$\Rightarrow N=\frac{1}{2x^2+2x+5}\leq \frac{2}{9}$

Vậy $N_{\max}=\frac{2}{9}$. Giá trị này đạt tại $x+\frac{1}{2}=0\Leftrightarrow x=\frac{-1}{2}$

\(P=14-\left(2x-5\right)^2\)

Có: \(\left(2x-5\right)^2\ge0\Rightarrow14-\left(2x-5\right)^2\le14\)

Dấu = xảy ra khi: \(\left(2x-5\right)^2=0\Rightarrow2x-5=0\Rightarrow x=\frac{5}{2}\)

Vậy: \(Max_P=14\) tại \(x=\frac{5}{2}\)

thanhs

dễ mà cũng hỏi

  2 x 2 + 10 - 1 = 2 x 2 + 5 x - 1 / 2 B = 2 x 2 + 2 . 5 / 2   x   + 5 / 2 2 - 5 / 2 2 - 1 / 2 = 2 x + 5 / 2 2 - 25 / 4 - 2 / 4 = 2 x + 5 / 2 2 - 27 / 2 = 2 x + 5 / 2 2 - 27 / 2 V ì   x + 5 / 2 2   ≥   0   n ê n   2 x + 5 / 2 2   ≥   0   ⇒ 2   x + 5 / 2 2 - 27 / 2 ≥ - 27 / 2

Suy ra: B ≥ - 27/2 .

B= -27/2 khi và chỉ khi x + 5/2 = 0 suy ra x = -5/2

Vậy B = -27/2 là giá trị nhỏ nhất tại x = - 5/2

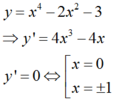
Hàm số đã cho liên tục trên 0 ; 2  có:

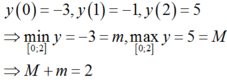
Chọn: A