1) Tìm x thuộc N thỏa :
16x<1284
NT
Những câu hỏi liên quan
Để bất phương trình
x
-
6
1
-
x
m
-
1
6
x
-
2
6
x...
Đọc tiếp
Để bất phương trình x - 6 1 - x m - 1 6 x - 2 6 x + 2 m + 1 ≥ 0 thỏa mãn với mọi x thuộc đoạn 0 ; 1
A. m ≥ 1 4
B. m ≤ 1 2
C. 1 4 ≤ m ≤ 1 2
D. m ≤ 1 3
Chọn B
Phương pháp: Đánh giá.
Cách giải: Với x=1 dễ thấy bất phương trình thỏa mãn với mọi m
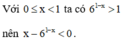
Do đó yêu cầu bài toán tương đương với
Đúng 0
Bình luận (0)
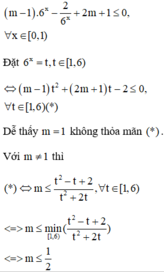
cho x;y thuộc N thỏa mãn: (16x+17y)(17x+16y) chia hết cho 11
CMR : (16x+17y)(17x+16y) chia hết cho 121
A= 16x+17y
B= 17x +16y Vì A.B chia hết cho 11 => A chia hết cho 11 hoặc B chia hết cho 11
ta có: 17 A -16B = 16.17x + 17.17y - 16.17x -16.16y = 33y chia hết cho 11
=>Nếu A chia hết cho 11 => B chia hết cho 11
hoặc B chia hết cho 11 => A chia hết cho 11
Vậy A và B chia hết cho 11
=> A.B chia hết cho 11.11 =121
Đúng 0
Bình luận (0)
tìm x thỏa mãn: x^4-2x^2-16x+1=0
Tìm số nguyên �x thỏa mãn �24.4.4.4x24.4.4.4.
�−16x−16 hoặc �16x16.
�−4x−4 hoặc �4x4.
�4x4.
�16x16.
Đọc tiếp
Tìm số nguyên thỏa mãn .
hoặc . hoặc . . .
Lời giải:
$x^2=4.4.4.4=16.16=(-16)(-16)=16^2=(-16)^2$
$\Rightarrow x=16$ hoặc $x=-16$.
Đúng 0
Bình luận (0)
tìm x thỏa mãn đẳng thức\(|x+1|+|2x+3|+|3x+5|=16x-1\)
lập bảng xét dấu là tính được
Đúng 0
Bình luận (0)
Tìm cặp (x; y) thỏa mãn: \(\left(16x^4+1\right)\left(y^4+1\right)=16x^2y^2\)
Ta có: \(16x^4+1\ge8x^2\) ; \(y^4+1\ge2y^2\)
\(\Rightarrow\left(16x^4+1\right)\left(y^4+1\right)\ge8x^2.2y^2=16x^2y^2\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}16x^4=1\\y^4=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\pm\frac{1}{2}\\y=\pm1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho hàm số f(x) có đạo hàm liên tục trên [-1;1] và thỏa f(1) 0,
f
x
2
+
4
f
x
8
x
2
+
16
x
-
8
với mọi x thuộc [-1;1]. Giá trị của
∫
0
1
f
x
d...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên [-1;1] và thỏa f(1) = 0, f ' x 2 + 4 f x = 8 x 2 + 16 x - 8 với mọi x thuộc [-1;1]. Giá trị của ∫ 0 1 f x d x bằng
A. 
.
B. 
.
C. 
.
D. 
.
1.Tìm x;y thuộc N : x^3 -7=y^2
2.Tìm p;q thuộc P và x thuộc z thỏa mãn: x^5+px+3q=0
3, Tìm x;y thuộc Z thỏa mãn 6x^3-xy(11x+3y)+2y^3=6
Cho x,y,z=0 thỏa mãn x^2+y^2+z^2=1 Tìm GTNN của M=1/16x^2+1/4y^2+1/z^2
x, y, z > 0 chứ bn ? Nếu đúng z thì inbox với mik, mik sẽ chỉ cho....
Đúng 0
Bình luận (0)
cho p là một số nguyên tố. n thuộc N, n≥1. Tìm x, y thuộc N thỏa mãn x(x+1)=p^(2n)y(y+1)