Một vật khối lượng 300g thực hiện đồng thời hai dao độngk là x1= 5 căn 3 cos(5 pi t) cm ; x2= 5 cos (5 pi t -alpha) cm. Biết phương trình dao động tổng hợp của vật x= A cos (5 pi t - beta) cm. Biết 0<beta<alpha<pi, alpha+beta=pi/2 . Năng lượng dao động của vật là
MH
Những câu hỏi liên quan
1.Tìm giao động tổng hợp của x1 3cosomega t cm và x2 4sin (omega t+dfrac{pi}{6}) cm .
2.Một vật có khối lượng 200g thực hiện đồng thời hai dao động điều hòa cùng phương, có phương trình là :
x1 3.cosleft(15t+dfrac{pi}{6}right)cm và x2 A_2.cosleft(15t+dfrac{pi}{2}right). Cơ năng của dao động là 0,06075J. Biên độ dao động của dao động thứ 2 là ?
3.Một vật thực hiện đồng thời hai dao động cùng phương có phương trình : x_15sqrt{2}cosleft(2pi t+dfrac{2pi}{3}right) cm và x_25sqrt{2}cosleft(2pi t-df...
Đọc tiếp
1.Tìm giao động tổng hợp của x1 = 3cos\(\omega t\) cm và x2 = 4sin (\(\omega t+\dfrac{\pi}{6}\)) cm .
2.Một vật có khối lượng 200g thực hiện đồng thời hai dao động điều hòa cùng phương, có phương trình là :
x1= \(3.cos\left(15t+\dfrac{\pi}{6}\right)cm\) và x2= \(A_2.cos\left(15t+\dfrac{\pi}{2}\right)\). Cơ năng của dao động là 0,06075J. Biên độ dao động của dao động thứ 2 là ?
3.Một vật thực hiện đồng thời hai dao động cùng phương có phương trình : \(x_1=5\sqrt{2}cos\left(2\pi t+\dfrac{2\pi}{3}\right)\) cm và \(x_2=5\sqrt{2}cos\left(2\pi t-\dfrac{2\pi}{3}\right)cm\) . Tìm pha của dao động tổng hợp .
Mọi người giải chi tiết giúp mình với nhé .
Một vật thực hiện đồng thời hai dao động thành phần: x1 10cos(πt + π/6)cm và x2 5 cos(πt + π/6)cm. Phương trình của dao động tổng hợp là: A. x 15cos(πt + π/6)cm. B. x 5cos(πt + π/6)cm. C. x 10cos(πt + π/6)cm. D. x 15cos(πt)cm.
Đọc tiếp
Một vật thực hiện đồng thời hai dao động thành phần: x1 = 10cos(πt + π/6)cm và x2 = 5 cos(πt + π/6)cm. Phương trình của dao động tổng hợp là:
A. x = 15cos(πt + π/6)cm.
B. x = 5cos(πt + π/6)cm.
C. x = 10cos(πt + π/6)cm.
D. x = 15cos(πt)cm.
Chọn A
+ Hai dao động cùng pha![]() và pha φ là pha của các dao động
và pha φ là pha của các dao động
=> x = 15cos(πt + π/6)cm.
Đúng 0
Bình luận (0)
một vật tham gia đồng thời hai dao điều hoà cùng phương có phương trình lần lượt là x1=6cos(wt) cm x2 = 6 căn 3 cos(wt+pi/2) pha ban đầu của dao động tổng hợp là
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, biểu thức có dạng
x
1
3
cos
(
2
πt
+
π
6
)
cm và
x
2
cos
(
2
πt
+
2
π
3
)
c...
Đọc tiếp
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, biểu thức có dạng x 1 = 3 cos ( 2 πt + π 6 ) cm và x 2 = cos ( 2 πt + 2 π 3 ) cm. Phương trình dao động tổng hợp là
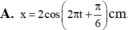
![]()
![]()
![]()
Cho 4 dao động đều cùng phương cùng tầ số góc có phương trình lần lượt là
x1= 10cos(20πt + π/3) cm; x2 = 6căn3cos(20π t) cm và x3 = 4căn3cos(20πt - π/2) cm; x4 = 10cos(20πt +2π/3) cm. Một vật có khối lượng 500 g thực hiện đồng thời bốn dao động trên. Xác định thời điểm
vật qua li độ x = -3căn6 cm lần thứ 9?
một vật thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là x15cos(wt + phi)cm và x2A2cos(wt- pi/4) thì dao động tổng hợp có phương trình dao động là xA cos(wt- pi/12). để biên độ A có giá trị bằng một nữa giá trị cực đại Amax của chính nó thì biên độ A2 có giá trị làA.5/căn 3 B.10/căn 3 C.10 căn 3 D.5 căn 3
Đọc tiếp
một vật thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là x1=5cos(wt + phi)cm và x2=A2cos(wt- pi/4) thì dao động tổng hợp có phương trình dao động là x=A cos(wt- pi/12). để biên độ A có giá trị bằng một nữa giá trị cực đại Amax của chính nó thì biên độ A2 có giá trị là
A.5/căn 3 B.10/căn 3 C.10 căn 3 D.5 căn 3
\(x_1 = 5 \cos (\omega t + \varphi)cm.\)
\(x_2 = A_2 \cos (\omega t - \frac{\pi}{4})cm.\)
\(x= A \cos (\omega t - \frac{\pi}{12})cm.\)
Vẽ giản đồ véc tơ như hình vẽ
Áp dụng định lý hàm số Sin ta có:
Xét: \(\triangle OA_1A:\) \(\frac{A}{\sin OA_1A} = \frac{A_1}{\sin OAA_1} \)
=> \(\frac{A}{\sin (\frac{3\pi}{4}-\varphi)} = \frac{A_1}{\sin (\frac{\pi}{6})} \)
=> \(A= \frac{A_1}{\sin (\frac{\pi}{6})} .\sin (\frac{3\pi}{4}-\varphi).(*)\)
TH1: \(A= A _{max} <=> \sin (\frac{3\pi}{4}-\varphi) = 1\)
=> \(A_{max}= \frac{A_1}{\sin (\frac{\pi}{6})}= 10cm.(1)\)
TH2: \(A = \frac{A_{max}}{2} => \sin (\frac{3\pi}{4}-\varphi) = \frac{1}{2}.\)
=> \(\frac{3\pi}{4} - \varphi = \frac{\pi}{6}\)
=> \(\varphi = \frac{7\pi}{12}.(2)\)
Xét: \(\triangle OA_2A:\) \(\frac{A}{\sin OA_2A} = \frac{A_2}{\sin OAA_2} \)
=> \(\frac{A}{\sin (\frac{3\pi}{4}-\varphi)} = \frac{A_2}{\sin (\varphi+\frac{\pi}{12})} \)
=> \(A_2= \frac{A_{max}}{\sin (\frac{3\pi}{4}-\varphi)} .\sin (\frac{\pi}{12}+\varphi).(3)\)
Thay \((1); (2)\) vào \((3)\) ta được: \(A_2= \frac{10}{0,5} .\sin (\frac{\pi}{12}+\frac{7\pi}{12}) = \frac{10}{0,5}.\frac{\sqrt{3}}{2} = 10 \sqrt{3}cm.\)
Chọn đáp án.C.\(10\sqrt{3}cm.\)
Đúng 0
Bình luận (0)
Bạn kiểm tra lại xem giả thiết còn thiếu gì không?
Đúng 0
Bình luận (0)
mình đánh đủ dữ kiện của đề rồi đó bạn :)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
một vật thực hiện đồng thời 2 dao động điều hòa cùng phương, cùng tần số có phương trình x1=\(\sqrt{3}cos\left(20\pi t-\frac{\pi}{2}\right)\left(cm\right)\)và x2=\(cos\left(20\pi t\right)\left(cm\right)\) xác định thời điểm đầu tiên vật đi qua li độ x=-1cm theo chiều dương. giúp mình với nhé...!! thanks
Một chất điểm có khối lượng m 300g đồng thời thực hiện hai dao động điều hòa cùng phương, cùng tần số. Ở thời điểm t bất kì li độ của hai dao động thành phần luôn thõa mãn
16
x
1
2
+
9
x
2
2
25
(x1, x2 tính bằng cm). Biết lực phục hồi cực đại tác dụng lên chất điểm trong quá t...
Đọc tiếp
Một chất điểm có khối lượng m = 300g đồng thời thực hiện hai dao động điều hòa cùng phương, cùng tần số. Ở thời điểm t bất kì li độ của hai dao động thành phần luôn thõa mãn 16 x 1 2 + 9 x 2 2 = 25 (x1, x2 tính bằng cm). Biết lực phục hồi cực đại tác dụng lên chất điểm trong quá trình dao động là
A. 10π rad/s
B. 8 rad/s
C. 4 rad/s
D. 4π rad/s
Đáp án B
Phương pháp : Sử dụng công thức tính biên đô ̣của dao động tổng hợp
Lực hồi phục cực đại: Fmax = mω2A
Cách giải :
Từ giả thuyết:
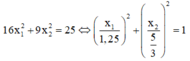
Hai dao động này vuông pha với các biên độ thành phần A1 = 0,8cm, A2 = 0,6cm
Biên độ dao động tổng hợp:
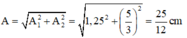
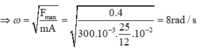
Mặt khác:
![]()
Đúng 0
Bình luận (0)
Một vật dao động điều hoà trên trục Ox, trong 2 s đầu nó thực hiện được 5 dao động và đi được quãng đường 1 m. Biết toạ độ ban đầu của vật là x 5 cm, phương trình dao động của vật làA.x10cos(10pi t) (cm)B.x5cos(5pi t) (cm)C.x10cos(10pi t - frac{pi}{3}) (cm)D.x5cos(10pi t) (cm)
Đọc tiếp
Một vật dao động điều hoà trên trục Ox, trong 2 s đầu nó thực hiện được 5 dao động và đi được quãng đường 1 m. Biết toạ độ ban đầu của vật là x = 5 cm, phương trình dao động của vật là
A.\(x=10\cos(10\pi t) \ (cm)\)
B.\(x=5\cos(5\pi t) \ (cm)\)
C.\(x=10\cos(10\pi t - \frac{\pi}{3}) \ (cm)\)
D.\(x=5\cos(10\pi t) \ (cm)\)
Phương trình tổng quát: \(x = A\cos(\omega t +\varphi)\)
+ Quãng đường khi vật thực hiện 5 dao động: S = 5.4A = 100 cm \(\Rightarrow\) A = 5cm.
+ Tần số: f = 5/2 = 2,5 Hz \(\Rightarrow \omega = 2\pi f = 2\pi.2,5 = 5\pi \ (rad/s)\)
+ t= 0 khi vật có x0=5 nên vật đang ở biên độ dương \(\Rightarrow \varphi = 0\)
Vậy phương trình dao động: \(x=5\cos(5\pi t) \ (cm)\)
Đúng 0
Bình luận (0)

