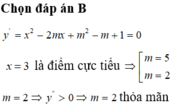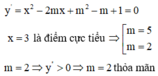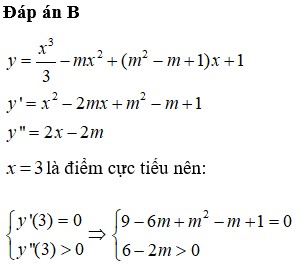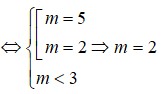tìm m để y = x3-mx2+(m-\(\frac{2}{3}\))x +5 đạt cực tiểu tại x =1
LT
Những câu hỏi liên quan
Bài 1. Cho hàm số: y 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x 1Bài 2. Cho hàm số y 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x -2 .Bài 3. Cho hàm số y 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x 2.Bài 4. Tìm tất cả tham số thực m để hàm số y (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tạix -1.Bài 5. Tìm giá trị của tham số m để hàm số y x3/3...
Đọc tiếp
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
Tìm m để hàm số
y
x
3
3
-
m
x
2
+
(
m
2
-
m
+
1
)
x
+
1
đạt cực tiểu tại
x
3
A.
m
5
B.
m
2
C.
m...
Đọc tiếp
Tìm m để hàm số y = x 3 3 - m x 2 + ( m 2 - m + 1 ) x + 1 đạt cực tiểu tại x = 3
A. m = 5
B. m = 2
C. m = 2 , m = 5
C. m = 4
Giá trị thực của tham số m để hàm số
y
-
x
3
+
m
x
2
+
m
2
-
12
x
+
2
đạt cực tiểu tại x -1 thuộc khoảng nào dưới đây? A. (3;6) B. (5;9) C. (0;3) D. (-4;0)
Đọc tiếp
Giá trị thực của tham số m để hàm số y = - x 3 + m x 2 + m 2 - 12 x + 2 đạt cực tiểu tại x = -1 thuộc khoảng nào dưới đây?
A. (3;6)
B. (5;9)
C. (0;3)
D. (-4;0)
Tìm m để hàm số
y
x
3
3
-
m
x
2
+
m
2
-
m
+
1
x
+
1
đạt cực tiểu tại
x
3
A. m 5 B. m 2 C.
m
2...
Đọc tiếp
Tìm m để hàm số y = x 3 3 - m x 2 + m 2 - m + 1 x + 1 đạt cực tiểu tại x = 3
A. m = 5
B. m = 2
C. m = 2 , m = 5
D. m = 4
Với giá trị nào của m thì hàm số y = x 3 - m x 2 - x + 1 đạt cực tiểu tại x = 1 ?
A. m = -1
B. m = 1
C. m = 2
D. m = -2
Tìm giá trị của tham số m để hàm số
a) y = x 3 + (m + 3) x 2 + mx – 2 đạt cực tiểu tại x = 1
b) y = −( m 2 + 6m) x 3 /3 − 2m x 2 + 3x + 1 đạt cực đại tại x = -1;
a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 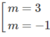
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
Đúng 0
Bình luận (0)
Tìm m để hàm số y x3�3 - 3mx2�2 + (m-1)x + 2 đạt cực tiểu tại x2
Đọc tiếp
Tìm m để hàm số y = - 3m + (m-1)x + 2 đạt cực tiểu tại x=2
\(y=x^3-3mx^2+\left(m-1\right)x+2\)
\(y'=3x^2-6mx+m-1\)
\(y''=6x-6=6\left(x-1\right)\)
Để hàm số trên đạt cực trị tại \(x_o=2\) khi và chỉ khi
\(\left\{{}\begin{matrix}y'\left(2\right)=0\\y''\left(2\right)>0\end{matrix}\right.\) \(\)
\(\Leftrightarrow\left\{{}\begin{matrix}12-12m+m-1=0\\6\left(2-1\right)=6>0\left(luôn.đúng\right)\end{matrix}\right.\)
\(\Leftrightarrow11m=11\)
\(\Leftrightarrow m=1\)
Vậy với \(m=1\) thỏa yêu cầu đề bài.
Đúng 1
Bình luận (2)
Tìm tất cả các giá trị của tham số m để hàm số
y
x
3
-
m
x
2
+
(
2
m
-
3
)
x
-
3
đạt cực đại tại ...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = x 3 - m x 2 + ( 2 m - 3 ) x - 3 đạt cực đại tại x = 1
A. m = 3
B. m > 3
C. m ≤ 3
D. m < 3
Chọn B
+ Để hàm số đạt cực đại x = 1 thì
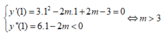
Đúng 0
Bình luận (0)
Tìm m để hàm số y = x 3 3 - m x 2 + ( m 2 - m + 1 ) x + 1 đạt cực tiểu x=3.
A. m= 5
B. m= 2
C. m= 2, m= 5
C. m= 4
Xác định m để hàm số: y = x 3 − m x 2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
∆ ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
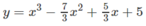
Ta có:
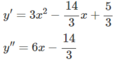
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y CT = y(1) = (16/3).
Đúng 0
Bình luận (0)