Gía trị của \(a^3-b^3\) thõa mãn
\(a-b=-1\) và a.b=7
VT
Những câu hỏi liên quan
Cho z,b,c là 3 số dương thõa mãn abc=1 Tìm gía trị nhỏ nhất của A= \(\frac{a^2}{1+b}+\frac{b^2}{1+c}+\frac{c^2}{1+a}\)
a)Giá trị x0 thõa mãnfrac{11}{14}+left|frac{2}{7}-xright|-frac{5}{2}frac{4}{3}b)giá trị của a thõa mãnfrac{a}{b}frac{-2.5}{4.5}và a+b1,44c)giá trị của b thõa mãnleft(frac{a}{b}right)^3frac{1}{1000}và b-a36d) giá trị x thõa mãn2divfrac{3}{5}-1frac{3}{4}divleft(frac{-9}{20}xright)e)giá trị biểu thức2.5timesleft(-3x+1right)^2-12left|xright|-9tại x-0,2
Đọc tiếp
a)Giá trị x>0 thõa mãn
\(\frac{11}{14}+\left|\frac{2}{7}-x\right|-\frac{5}{2}=\frac{4}{3}\)
b)giá trị của a thõa mãn
\(\frac{a}{b}=\frac{-2.5}{4.5}\)và a+b=1,44
c)giá trị của b thõa mãn
\(\left(\frac{a}{b}\right)^3=\frac{1}{1000}\)và b-a=36
d) giá trị x thõa mãn
\(2\div\frac{3}{5}=-1\frac{3}{4}\div\left(\frac{-9}{20}x\right)\)
e)giá trị biểu thức
\(2.5\times\left(-3x+1\right)^2-12\left|x\right|-9\)
tại x=-0,2
Cho a,b là hai số thực thõa mãn a.b>0
Khi đó, giá trị nhỏ nhất của biểu thức Q=(a+b)(1/a+1/b), Qmin=?
(a+b)(1/a+1/b)=1+a/b+b/a+1
=2+(a^2+b^2)/(a*b)
vì a^2+b^2>0; a*b>0
=>Qmin=2
Đúng 0
Bình luận (0)
cho a:b=2:5 ; b:c=4:3 và a.b-c.c=-10,4. Gía trị của giá trị tyệt đối của a+b+c
Gía trị của x thõa mãn: 2x+1/5 = 3y-2/7 = 2x+3y-1/6x
Xét hai số phức
z
1
,
z
2
thay đổi thõa mãn
z
1
-
z
2
z
1
+
z
2
+
4...
Đọc tiếp
Xét hai số phức z 1 , z 2 thay đổi thõa mãn z 1 - z 2 = z 1 + z 2 + 4 - 2 i = 2 . Gọi A, B lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức z 1 2 + z 2 2 . Gía trị của AB là
A. 110
B. 116
C. 112
D. 114
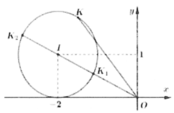
Gọi M, N, K, I lần lượt biểu diễn số phức
Đúng 0
Bình luận (0)
tìm cặp (a;b) nguyên sao cho a.b lớn nhất thõa mãn (a+1)(b+2)=3
trả lời ; a=...........b=
cho x≠0 thõa mãn x=\(\dfrac{1}{x}=a\) là một hằng số .Tính theo a giá trị của biểu thức :
\(A=x^3+\dfrac{1}{x^3}\), \(B=x^6+\dfrac{1}{x^6}\), \(C=x^7+\dfrac{1}{x^7}\)
Sửa đề: \(x+\dfrac{1}{x}=a\)
\(A=x^3+\dfrac{1}{x^3}=\left(x+\dfrac{1}{x}\right)^3-3\left(x+\dfrac{1}{x}\right)=a^3-3a\\ B=x^6+\dfrac{1}{x^6}=\left(x^3+\dfrac{1}{x^3}\right)^2-2=\left(a^3-3a\right)^2-2=a^6-6a^4+9a^2-2\\ C=x^7+\dfrac{1}{x^7}=\left(x^3+\dfrac{1}{x^3}\right)\left(x^4+\dfrac{1}{x^4}\right)-\left(x+\dfrac{1}{x}\right)\)
Mà \(x^4+\dfrac{1}{x^4}=\left(x^2+\dfrac{1}{x^2}\right)^2-2=\left[\left(x+\dfrac{1}{x}\right)^2-2\right]^2-2=\left(a^2-2\right)^2-2=a^4-4a^2+2\)
\(\Leftrightarrow C=\left(a^3-3a\right)\left(a^4-4a^2+2\right)-a=...\)
Đúng 2
Bình luận (1)
Cho a,b là hai số thực thõa mãn a.b>0. Tính giá trị nhỏ nhất của biểu thức: \(Q=\left(a+b\right)\left(\frac{1}{a}+\frac{1}{b}\right)\)
gtnn=4 dok pn k nka. đảm bảo đúg lun mjk vừa làm xog
Đúng 0
Bình luận (0)
Bạn nhân hai biểu thức rồi dùng bất đẳng thức cô-si.suy ra min=4
Đúng 0
Bình luận (0)