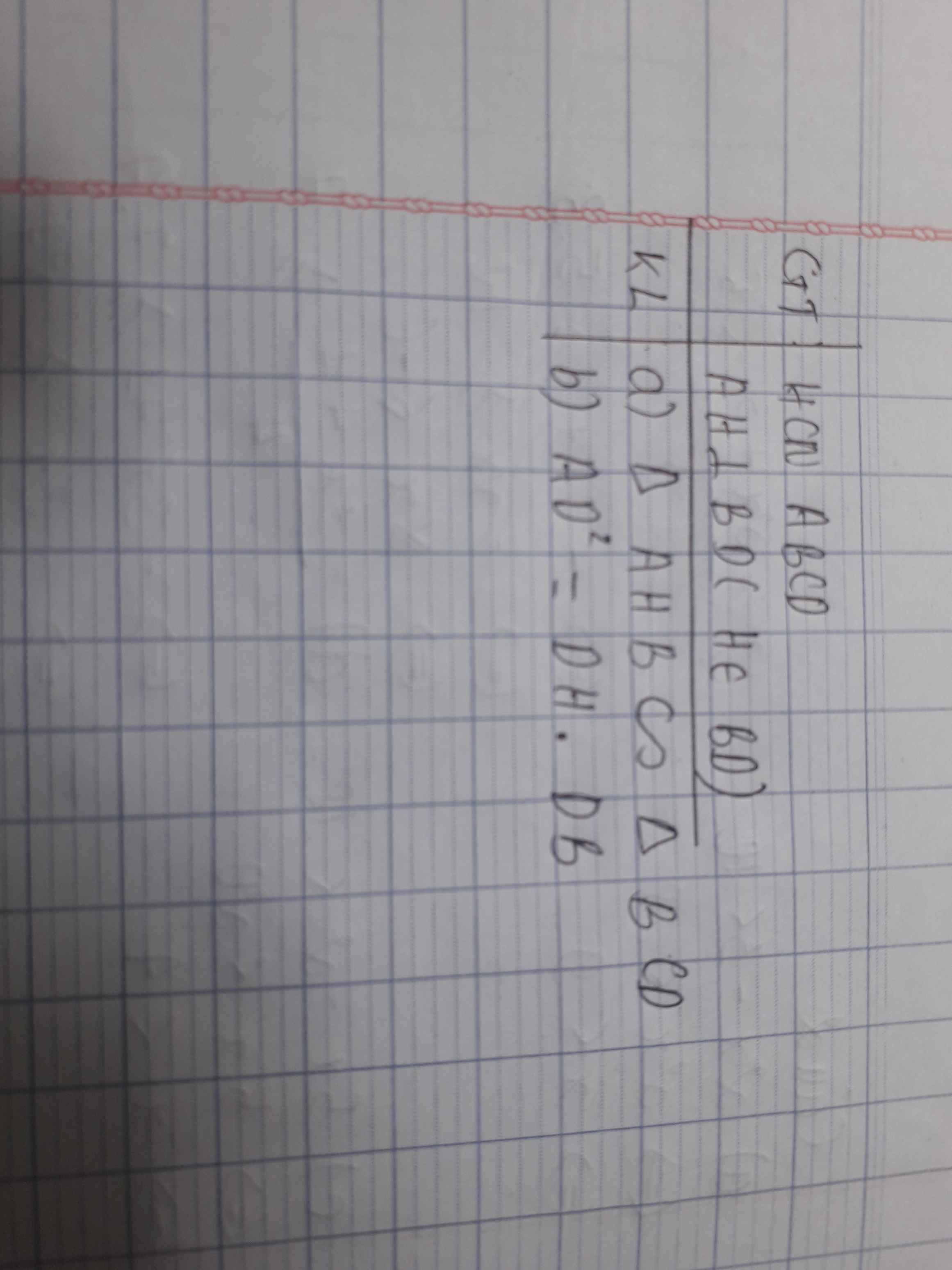Chỉ cần viết giả thuyết và kết luận thôi 
H24
Những câu hỏi liên quan
A) Hãy viết định lí nói về 1 đường thẳng vuông góc với một trong hai đường thẳng song song
B) Vẽ hình minh họa định lí đó và viết giả thiết,kết luận bằng kí hiệu
chỉ cần ghi định lí,giả thiết,kết luận thôi!
Giúp mik ( Chỉ cần giúp giả thiết kết luận của hình trên thôi ạ) mik cảm ơn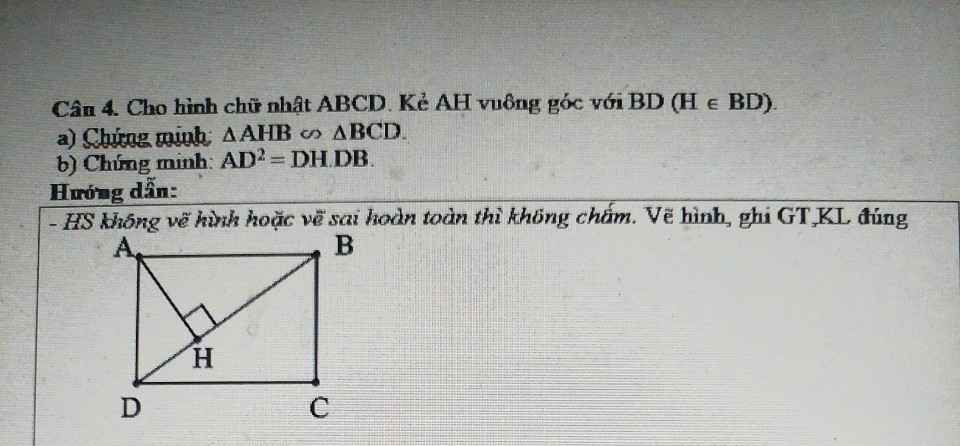
cứu em chỉ cần ghi giả thuyết và kết luận thui =))
cho tam giác ABC cân tại A vẽ AH vuông góc với BC tại H
khỏi ghi kết luận giả thuyết thôi đc rồi =)))
Đúng 0
Bình luận (0)
GT:
△ABC cân tại A
AH ⊥ BC tại H
Làm gì có KL?
Đúng 1
Bình luận (0)
vẽ 1 hình tam giác ABC có cạnh 6 cm và bằng nhau
và viết giả thuyết kết luận và lời giải
help bài này cần gấp
Câu 3 câu H(x) thôi ạ còn câu 4,5 vẽ hình nêu giả thuyết kết luận
Bài 5:
a) Xét ΔABM vuông tại A và ΔEBM vuông tại E có
BM chung
\(\widehat{ABM}=\widehat{EBM}\)(BM là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABM=ΔEBM(cạnh huyền-góc nhọn)
Đúng 1
Bình luận (0)
Bài 5:
b) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc ở đáy)
\(\Leftrightarrow\widehat{MCB}+60^0=90^0\)
hay \(\widehat{MCB}=30^0\)(1)
Ta có: BM là tia phân giác của \(\widehat{ABC}\)(gt)
nên \(\widehat{MBC}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)(2)
Từ (1) và (2) suy ra \(\widehat{MBC}=\widehat{MCB}\)
Xét ΔMBC có \(\widehat{MBC}=\widehat{MCB}\)(cmt)
nên ΔMBC cân tại M(Định lí đảo của tam giác cân)
Suy ra: MB=MC(Hai cạnh bên)
Xét ΔMBE vuông tại E và ΔMCE vuông tại E có
MB=MC(cmt)
ME chung
Do đó: ΔMBE=ΔMCE(cạnh huyền-cạnh góc vuông)
Suy ra: BE=CE(Hai cạnh tương ứng)
Đúng 0
Bình luận (0)
nhớ viết giả thuyết kết luận ko viết cũng đc
Đọc tiếp
nhớ viết giả thuyết kết luận ko viết cũng đc
3:
a: BC^2=AB^2+AC^2
=>ΔABC vuông tại A
b: Xét ΔBCD có
BA vừa là đường cao, vừa là trung tuyến
=>ΔBCD cân tại B
c: OA=1/3*BA=1cm
OC=căn 4^2+1^2=căn 17(cm)
Đúng 0
Bình luận (0)
tứ giác ABCD có AB=BC và AC là tia phân giác của góc A . Chứng minh rằng ABCD là hình thang (viết giả thuyết và kết luận với vẽ hình)
giúp mik vs ạ mik đag cần gắp m.người ơi
m.người ơi
Xem chi tiết
giúp mik vs ạ mik đag cần gắp
BA=BC
=>góc BAC=góc BCA
=>góc BCA=góc DAC
=>AD//BC
=>ABCD là hình thang
Đúng 0
Bình luận (0)
giúp mình vẽ tia phân giác và ghi giả thiết và kết luận hộ mình thôi ko cần giải bài cũng được mình hứa sẽ cho 5 sao
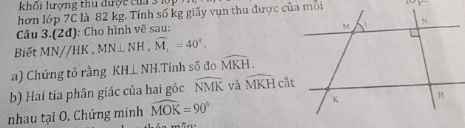
a: MN//HK
MN⊥NH
Do đó: HK⊥NH
Đúng 1
Bình luận (0)
Giúp em câu này với mọi người oi
Viết giả thuyết kết luận giùm em luôn nha
a: Ta có: A và B đối xứng nhau qua Ox
nên OA=OB(1)
Ta có: A và C đối xứng nhau qua Oy
nên OA=OC(2)
Từ (1) và (2) suy ra OB=OC
hay ΔOBC cân tại O
Đúng 0
Bình luận (1)