Viết phương trình mặt phẳng (P) đi qua H(1;2;1) và lần lượt cắt Ox, Oy, Oz tại A, B, C sao cho H là trực tâm của tam giác ABC
DH
Những câu hỏi liên quan
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
1. Viết phương trình mặt phẳng (P) đi qua và tiếp xúc với (S) A.
3
x + 4z - 2 0 B.
3
y + z - 2 0 C. y +
3
z 0 D. x +
3
y + z - 2 0
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
= 1. Viết phương trình mặt phẳng (P) đi qua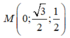 
và tiếp xúc với (S)
A. 3 x + 4z - 2 = 0
B. 3 y + z - 2 = 0
C. y + 3 z = 0
D. x + 3 y + z - 2 = 0
Đề số 1:
Bài tập 4: Trong không gian cho M (1 ; 2 ; 3) N (- 3 ; 4 ; 1).
P x + 2y - z + 4 = 0
a, Viết phương trình mặt phẳng trung trực MN
b, Viết phương trình mặt phẳng \(\left(\beta\right)\) đi qua MN và song song (P)
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(0;1;3) và song song với mặt phẳng
(
Q
)
:
2
x
-
3
z
+
1
0
.
A. 2x - 3z - 10 0 B. 2x + 3z – 9 0 C. 2x - 3z + 9 0 D. 2x + 3z + 1 0
Đọc tiếp
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(0;1;3) và song song với mặt phẳng ( Q ) : 2 x - 3 z + 1 = 0 .
A. 2x - 3z - 10 = 0
B. 2x + 3z – 9 = 0
C. 2x - 3z + 9 = 0
D. 2x + 3z + 1 = 0
Chọn C.
Mặt phẳng (P) song song với mặt phẳng (Q):2x - 3z + 1 = 0 nên mặt phẳng (P) có phương trình dạng: 2x - 3z + D = 0 (D ≠ 1).
Mặt phẳng (P) đi qua điểm M nên thay tọa độ điểm vào phương trình mặt phẳng (P) ta được:
2.0 - 3.3 + D = 0 ⇔ D = 9 (thỏa mãn D ≠ 1).
Vậy phương trình mặt phẳng (P) là: 2x - 3z + 9 = 0.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm
M
(
0
;
1
;
3
)
và song song với mặt phẳng
(
Q
)
:
2
x
–
3
z
+
1
0
.
A. 2x - 3z + 2 0 B. 2x- 3z + 9 0 C. 2x + 3z – 9 0 D. Đáp án khác
Đọc tiếp
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M ( 0 ; 1 ; 3 ) và song song với mặt phẳng ( Q ) : 2 x – 3 z + 1 = 0 .
A. 2x - 3z + 2 = 0
B. 2x- 3z + 9 = 0
C. 2x + 3z – 9 = 0
D. Đáp án khác
Chọn B
Mặt phẳng (P) song song với mặt phẳng (Q): 2x – 3z + 1 = 0 nên mặt phẳng (P) có phương trình dạng: 
.
Mặt phẳng (P) đi qua điểm M(0;1;3) nên thay tọa độ điểm vào phương trình mặt phẳng (P) Ta được: 2.0 -3.3 + D = 0 ⇔ D = 9 (thỏa mãn D ≠ 1).
Vậy phương trình mặt phẳng (P) là: 2x – 3z + 9 = 0.
Đúng 0
Bình luận (0)
Viết phương trình mặt phẳng (P) đi qua điểm A (0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 0. A. (P) : 2y + 2z - 1 0 B. (P) : y + z - 1 0 C. (P) : y - z + 3 0 D. (P) : 2x + z - 2 0
Đọc tiếp
Viết phương trình mặt phẳng (P) đi qua điểm A (0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 = 0.
A. (P) : 2y + 2z - 1 = 0
B. (P) : y + z - 1 = 0
C. (P) : y - z + 3 = 0
D. (P) : 2x + z - 2 = 0
Viết phương trình mặt phẳng (P) đi qua điểm A(0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 0.
Đọc tiếp
Viết phương trình mặt phẳng (P) đi qua điểm A(0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 = 0.
Cho mặt phẳng
(
P
)
:
x
-
y
+
2
z
-
6
0
và điểm M(1;-1;2). Viết phương trình đường thẳng đi qua M và vuông góc với mặt phẳng (P). A.
x
-
1
1
y
+
1
2...
Đọc tiếp
Cho mặt phẳng ( P ) : x - y + 2 z - 6 = 0 và điểm M(1;-1;2). Viết phương trình đường thẳng đi qua M và vuông góc với mặt phẳng (P).
A. x - 1 1 = y + 1 2 = z - 2 - 1
B. x - 1 2 = y + 1 1 = z - 2 - 1
C. x - 1 1 = y + 1 - 1 = z - 2 2
D. x - 1 - 1 = y + 1 1 = z - 2 2
Viết phương trình mặt phẳng (P) đi qua ba điểm A(-3;0;0), B(0;-2;0), C(0;0;-1). A.
2
x
+
3
y
+
6
z
+
6
0
B.
2
x
-
3
y
+
6
z
+
6
0
C.
x
3
+...
Đọc tiếp
Viết phương trình mặt phẳng (P) đi qua ba điểm A(-3;0;0), B(0;-2;0), C(0;0;-1).
A. 2 x + 3 y + 6 z + 6 = 0
B. 2 x - 3 y + 6 z + 6 = 0
C. x 3 + y 2 + z 1 = 1
D. x 3 + y 2 + z 1 = 0
Hãy viết phương trình mặt phẳng (α) đi qua điểm M(2; -1; 2) và song song với mặt phẳng (β) : 2x – y + 3z + 4 = 0
Vì mặt phẳng (α) song song với mặt phẳng ( β) : 2x – y + 3z + 4 = 0 nên phương trình của mp(α) có dạng 2x – y + 3z + D = 0
Vì M(2; -1; 2) ∈ mp(α) nên 4 + 1 + 6 + D = 0 <=> D = -11
Vậy phương trình của mp(α) là: 2x – y + 3z - 11= 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho điểm
M
1
;
0
;
6
và mặt phẳng
α
có phương trình là
x
+
2
y
+
2
z
−
1
0
. Viết phương trình mặt phẳng
β
đi qua M và song song với
α
A.
β...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm M 1 ; 0 ; 6 và mặt phẳng α có phương trình là x + 2 y + 2 z − 1 = 0 . Viết phương trình mặt phẳng β đi qua M và song song với α
A. β : x + 2 y + 2 z + 13 = 0.
B. β : x + 2 y + 2 z − 15 = 0.
C. β : x + 2 y + 2 z − 13 = 0.
D. β : x + 2 y + 2 z + 15 = 0.
