Cho hình chóp S.ABC có đáy là tam giác vuông tại B,
SA= SB =2a, ASB = 60, bSC =90, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 45 . tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
Cho hình chóp S.ABC có đáy là tam giác vuông tại B,
SA= SB =2a, ASB = 60, bSC =90, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 45 . tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
Mình không thạo vẽ hình trên này nên bạn tự vẽ hình nhé.
Gọi K là hình chiếu vuông góc của S trên BC.
Giả sử \(\overrightarrow{CK}=x\overrightarrow{CB}\left(0< x< 1\right)\)
Đặt \(SC=ka\Rightarrow\left\{{}\begin{matrix}BC=a\sqrt{k^2+4}\\AC=a\sqrt{k^2+8}\end{matrix}\right.\)
Ta có: \(\dfrac{1}{SK^2}=\dfrac{1}{SB^2}+\dfrac{1}{SC^2}=\dfrac{1}{\left(2a\right)^2}+\dfrac{1}{\left(ka\right)^2}\)
\(\Rightarrow SK=\dfrac{2ka}{\sqrt{k^2+4}}\)
Ta có:
\(\left(\left(SBC\right);\left(ABC\right)\right)=45^0\)
\(\Rightarrow\left(AB;SK\right)=45^0\)
\(\Leftrightarrow\dfrac{\overrightarrow{AB}.\overrightarrow{SK}}{AB.SK}=cos45^0\Leftrightarrow\dfrac{\overrightarrow{AB}.\overrightarrow{SK}}{AB.SK}=\dfrac{\sqrt{2}}{2}\)
Lại có:
\(\overrightarrow{AB}.\overrightarrow{SK}=\left(\overrightarrow{SB}-\overrightarrow{SA}\right).\left[x\overrightarrow{SB}+\left(1-x\right)\overrightarrow{SC}\right]\)
\(=xSB^2-x\overrightarrow{SA}.\overrightarrow{SB}+\left(x-1\right).\overrightarrow{SC}.\overrightarrow{SA}\)
\(=x.4a^2-x.4a^2.\dfrac{1}{2}+\left(x-1\right).\dfrac{4a^2+k^2a^2-a^2\left(k^2+8\right)}{2}\)
\(=2xa^2+\left(x-1\right).\left(-2a^2\right)=2a^2\)
\(\Rightarrow\dfrac{\sqrt{2}}{2}=\dfrac{2a^2}{2a.\dfrac{2ka}{\sqrt{k^2+4}}}\Leftrightarrow k=2\)
Do đó:
\(\left\{{}\begin{matrix}SC=2a\\BC=2a\sqrt{2}\\AC=2a\sqrt{3}\end{matrix}\right.\)
Ta có:
\(R=\sqrt{R_{SAB}^2+R_{ABC}^2-\dfrac{AB^2}{4}}\)
\(=\sqrt{\left(\dfrac{2a\sqrt{3}}{3}\right)^2+\left(a\sqrt{3}\right)^2-\dfrac{\left(2a\right)^2}{4}}=\dfrac{a\sqrt{30}}{3}\)
\(\Rightarrow S=4\pi R^2=4\pi.\dfrac{10}{3}a^2=\dfrac{40}{3}\pi a^2\)
dạ em nhờ các anh chị, các bạn giải giúp mình bài toán này với ạ!
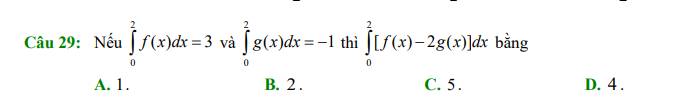
Giải giúp mình với ạ.
Câu 29 trong đề thi thử tốt nghiệp THPT môn Toán năm 2023 trường THPT Trần Phú, Đà Nẵng – CÓ ĐÁP ÁN: https://dethitoan.com.vn/de-thi-thu-tot-nghiep-thpt-mon-toan-nam-2023-truong-thpt-tran-phu-da-nang-co-dap-an/
\(\int\limits^2_0\left[f\left(x\right)-2g\left(x\right)\right]dx=\int\limits^2_0f\left(x\right)dx-2\int\limits^2_0g\left(x\right)dx=3+2=5\)

Các bạn giải hộ mình câu này với !
Trích: Đề thi học kì 1 lớp 12 môn Toán 2022 – 2023 sở GD_ĐT Hậu Giang
(link đề: https://dethitoan.com.vn/de-thi-hoc-ki-1-lop-12-mon-toan-2022-2023-so-gd_dt-hau-giang-co-dap-an-2/)
\(V=\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}\pi.2^2.3=4\pi\)
Chọn B
Một học sinh A lên kế hoạch tiết kiệm tiền để gửi đi làm từ thiện cho trẻ em vùng cao bằng cáchgửi ngân hàng với lãi suất không đổi 0.7% / tháng. Ban đầu, học sinh A có 1 triệu gửi ngân hàng từ đầu tháng và sau đó đúng 1 tháng thì mỗi tháng em lại gửi thêm vào 100.000 đồng. Tiền lãi hàng tháng học sinh A không rút mà cùng với tiền góp thêm 100.000 mỗi tháng thành gốc của
tháng tiếp theo. Hỏi sau 12 tháng học sinh A có bao nhiêu tiền để gửi đi làm từ thiện?
Ông Nam dự định mua một chiếc xe tải sau đó cho thuê. Dự tính số tiền thu được từ cho thuê chiếc xe tải đó hàng năm (tính đến cuối năm) là 200 triệu đồng. Sau 3 năm hoạt động sẽ thanh lý chiếc xe này với giá bán thanh lý (sau thuế) dự kiến là 5 triệu đồng. Hãy xác định xem Ông Nam chỉ có thể mua chiếc xe tải đó với giá tối đa bao nhiêu? Biết rằng:Lãi suất ngân hàng ổn định ở mức 5% /năm.
Gọi PV là giá trị hiện tại của dòng tiền thu được từ cho thuê và giá bán thanh lý. Ta có:
`PV = \frac{200}{(1+0.05)^1} + \frac{200}{(1+0.05)^2} + \frac{200}{(1+0.05)^3} + \frac{5}{(1+0.05)^3}`
`= \frac{200}{1.05} + \frac{200}{1.1025} + \frac{200}{1.1576} + \frac{5}{1.1576}`
Suy ra:
`PV ≈ 190.48 + 181.41 + 172.98 + 4.32`
<=> `PV ≈ 549.19`
Vậy, giá tối đa mà Ông Nam có thể mua chiếc xe tải là khoảng 549.19 triệu đồng.
Để xác định giá tối đa mà Ông Nam có thể mua chiếc xe tải đó, chúng ta cần tính giá trị hiện tại (PV) của dòng tiền thu được từ cho thuê và giá trị hiện tại (PV) của giá bán thanh lý sau 3 năm.
Giá trị hiện tại của dòng tiền thu được từ cho thuê hàng năm là 200 triệu đồng và sẽ kéo dài trong 3 năm. Vì lãi suất ngân hàng là 5% / năm, chúng ta có thể sử dụng công thức tính giá trị hiện tại của một chuỗi dòng tiền đều (annuity):
PV = PMT * ((1 - (1 + r)^(-n)) / r)
Trong đó: PV là giá trị hiện tại của chuỗi dòng tiền. PMT là dòng tiền hàng năm. r là lãi suất trong mỗi kỳ (tính theo tháng, quý hoặc năm). n là số kỳ (tháng, quý hoặc năm).
Áp dụng vào trường hợp này, chúng ta có: PMT = 200 triệu đồng r = 5% / năm = 0.05 n = 3 năm
Thay vào công thức, ta tính được: PV = 200 triệu * ((1 - (1 + 0.05)^(-3)) / 0.05) PV ≈ 578.19 triệu đồng
Giá trị hiện tại của giá bán thanh lý sau 3 năm là 5 triệu đồng. Chúng ta không cần điều chỉnh giá trị này vì nó đã được tính toán sau thuế.
Tổng cộng, giá trị hiện tại của chiếc xe tải là: PV_total = PV + Giá trị hiện tại giá bán thanh lý PV_total = 578.19 triệu + 5 triệu PV_total ≈ 583.19 triệu đồng
Do đó, Ông Nam chỉ có thể mua chiếc xe tải với giá tối đa khoảng 583.19 triệu đồng để đảm bảo thu hồi vốn và có lợi nhuận từ việc cho thuê xe tải trong 3 năm.
Tìm min f(x,y) = x+y với điều kiện (x-1)2 + y2 <=1 và x2 + y2 <=2
Các bạn giúp dùm mình với....
cho hàm số y=x^4 +8x^2 +m có giá trị nhỏ nhất trên [1;3] bằng 6 tham só thực m bằng
Hàm trùng phương có \(a>0;b>0\) nên đồng biến trên \(\left(0;+\infty\right)\)
\(\Rightarrow\min\limits_{\left[1;3\right]}y=y\left(1\right)=m+9\)
\(\Rightarrow m+9=6\Rightarrow m=-3\)
Bài tập về nhà: Nhà trường muốn đánh giá số giờ tự học của sinh viên trong tuần, để biết điều này phòng đào tạo chọn ngẫu nhiên 25 sinh viên và nhận được kết quả sau:
(các cột tương ứng như sau)
Số giờ tự học (giờ) 2 3 4 5 6 7 8 9 11
Số sinh viên 2 1 3 1 5 5 5 2 1
a) Hãy ước lượng số giờ tự học trung bình của sinh viên trong tuần với độ tin cậy
95%.
b) Với mức ý nghĩa 2% có thể cho rằng số giờ tự học trung bình của sinh viên trong tuần là 8 giờ được không?
Khảo sát sự hội tụ phân kỳ của tích phân suy rộng
\(\int\limits^{\infty}_0\dfrac{\ln\left(\sqrt[3]{1+\dfrac{3}{4}x^{200}}\right)}{x^2}dx\)
Help me