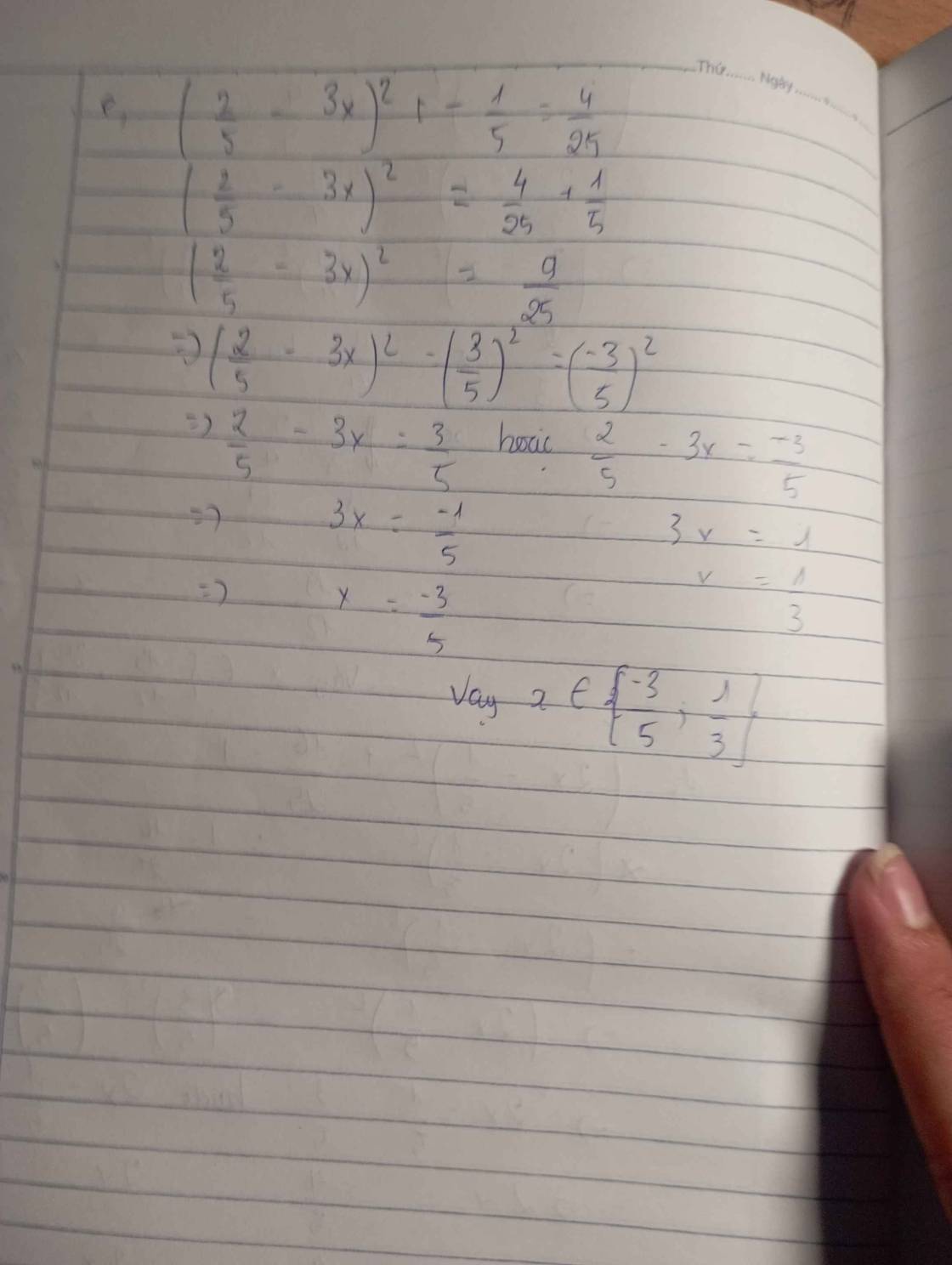a) \(\left(2\dfrac{3}{4}-1\dfrac{4}{5}\right)\cdot x=1\)

\(\left(\dfrac{11}{4}-\dfrac{9}{5}\right)\cdot x=1\)

\(\dfrac{19}{20}x=1\)

\(x=\dfrac{20}{19}\)

Vậy \(x=\dfrac{20}{19}\)

b) \(\left(x^2-9\right)\left(3-5x\right)=0\)

TH1:

\(x^2-9=0\)

\(x^2=9\)

\(x^2=3^2=\left(-3\right)^2\)

=>\(x\in\left\{3;-3\right\}\)

TH2:

\(3-5x=0\)

\(5x=3\)

\(x=\dfrac{3}{5}\)

Vậy \(x\in\left\{3;-3;\dfrac{3}{5}\right\}\)

bạn viết lại câu b được không?

1:

a: =7/5(40+1/4-25-1/4)-1/2021

=21-1/2021=42440/2021

b: =5/9*9-1*16/25=5-16/25=109/25

a)\(x=\left(\dfrac{3}{56}\cdot\dfrac{28}{9}\right):\dfrac{-3}{7}=\dfrac{1}{6}:\dfrac{-3}{7}=-\dfrac{7}{18}\)

b)\(x=\left(\dfrac{7}{15}\cdot\dfrac{5}{3}\right)+\dfrac{3}{16}=\dfrac{7}{9}+\dfrac{3}{16}=\dfrac{139}{144}\)

c)\(x=\left(\dfrac{5}{6}-\dfrac{2}{5}\right).5=\dfrac{13}{6}\)

d)\(=>x\left(\dfrac{3}{4}-\dfrac{2}{5}\right)=\dfrac{1}{6}\cdot\left(\dfrac{3}{7}+\dfrac{5}{7}\right)\)

\(x\cdot\dfrac{7}{20}=\dfrac{4}{21}=>x=\dfrac{4}{21}\cdot\dfrac{20}{7}=\dfrac{80}{147}\)

\(\left(\dfrac{3}{4}x-\dfrac{9}{16}\right)\left(\dfrac{1}{3}-\dfrac{3}{5}:x\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}\dfrac{3}{4}x-\dfrac{9}{16}=0\\\dfrac{1}{3}-\dfrac{3}{5}:x=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}\dfrac{3}{4}x=\dfrac{9}{16}\\\dfrac{3}{5}:x=\dfrac{1}{3}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=\dfrac{9}{5}\end{matrix}\right.\)

\(\left(\dfrac{3}{4}x-\dfrac{9}{16}\right)\left(\dfrac{1}{3}-\dfrac{3}{5}:x\right)=0\)

\(\Rightarrow\left(\dfrac{3}{4}x-\dfrac{9}{16}\right)\left(\dfrac{1}{3}-\dfrac{5}{3}x\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}\dfrac{3}{4}x-\dfrac{9}{16}=0\\\dfrac{1}{3}-\dfrac{5}{3}x=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}\dfrac{3}{4}x=\dfrac{9}{16}\Rightarrow x=\dfrac{3}{4}\\\dfrac{5}{3}x=\dfrac{1}{3}\Rightarrow x=\dfrac{1}{5}\end{matrix}\right.\)

c.\(\dfrac{3}{7}+\dfrac{5}{7}:x=\dfrac{1}{3}\)

\(\dfrac{5}{7}:x=\dfrac{1}{3}-\dfrac{3}{7}\)

\(\dfrac{5}{7}:x=-\dfrac{2}{21}\)

\(x=\dfrac{5}{7}:-\dfrac{2}{21}\)

\(x=-\dfrac{15}{2}\)

d.\(3\dfrac{1}{4}:\left|2x-\dfrac{5}{12}\right|=\dfrac{39}{16}\)

\(\left|2x-\dfrac{5}{12}\right|=3\dfrac{1}{4}:\dfrac{39}{16}\)

\(\left|2x-\dfrac{5}{12}\right|=\dfrac{4}{3}\)

\(\rightarrow\left[{}\begin{matrix}2x-\dfrac{5}{12}=\dfrac{4}{3}\\2x-\dfrac{4}{12}=-\dfrac{4}{3}\end{matrix}\right.\) \(\rightarrow\left[{}\begin{matrix}2x=\dfrac{7}{4}\\2x=-\dfrac{11}{12}\end{matrix}\right.\) \(\rightarrow\left[{}\begin{matrix}x=\dfrac{7}{8}\\x=-\dfrac{11}{24}\end{matrix}\right.\)

A, \(\dfrac{4}{9}+x=\dfrac{5}{3}\)

\(x\)\(=\dfrac{5}{3}-\dfrac{4}{9}\)

\(x\)\(=\dfrac{11}{9}\)

B,\(\dfrac{3}{4}.x=\dfrac{-1}{2}\)

\(x=\dfrac{-1}{2}:\dfrac{3}{4}\)

\(x=\)\(\dfrac{-2}{3}\)

a)

\(\frac{4}{9} + x = \frac{5}{3}\)

=> \(x = \frac{5}{3}-\frac{4}{9}\)

=> \(x = \) \(\frac{11}{9}\)

Vậy \(x = \dfrac{11}{9}\)

b) 

\(\dfrac{3}{4} .x = \dfrac{-1}{2}\)

=> \(x = \dfrac{-1}{2} : \dfrac{3}{4}\)

=> \(x = \dfrac{-2}{3}\)

Vậy \(x = \dfrac{-2}{3}\)

c)

\( \dfrac{3}{7}+ \dfrac{5}{7}:x = \dfrac{1}{3}\)

=> \(\dfrac{5}{7}:x = \dfrac{1}{3}-\) \( \dfrac{3}{7}\)

=> \(\dfrac{5}{7}:x = \dfrac{-2}{21}\)

=> \(x = \dfrac{5}{7}:\dfrac{-2}{21}\)

=> \(x = \dfrac{-15}{2}\)

Vậy \(x = \dfrac{-15}{2}\)

d) 

\(3\dfrac{1}{4} : |2x - \dfrac{5}{12} | = \dfrac{39}{16}\)

=> \(\dfrac{13}{4} : |2x - \dfrac{5}{12} | = \dfrac{39}{16}\)

=> \( |2x - \dfrac{5}{12} | =\dfrac{13}{4} : \dfrac{39}{16}\)

=> \(|2x-\dfrac{5}{12} |= \dfrac{4}{3}\)

=> \(\left[\begin{matrix} 2x - \dfrac{5}{12} = \dfrac{4}{3}\\ 2x - \dfrac{5}{12} = \dfrac{4}{3}\end{matrix}\right.\)

=> \(\left[\begin{matrix} 2x = \dfrac{-4}{3}+\dfrac{5}{12}\\ 2x = \dfrac{-4}{3}+\dfrac{5}{12} \end{matrix}\right.\)

=> \(\left[\begin{matrix} 2x = \dfrac{7}{4}\\ 2x = \dfrac{-11}{12} \end{matrix}\right.\)

=> \(\left[\begin{matrix} x = \dfrac{7}{8}\\ x = \dfrac{-11}{24} \end{matrix}\right.\)

Vậy \(x \in \) { \(\dfrac{7}{8} ; \dfrac{-11}{24}\) }

b: \(\left(\dfrac{2}{5}-\dfrac{7}{10}x\right):\dfrac{5}{3}=-\dfrac{3}{4}\)

\(\Leftrightarrow\dfrac{2}{5}-\dfrac{7}{10}x=\dfrac{-3}{4}\cdot\dfrac{5}{3}=\dfrac{-5}{4}\)

\(\Leftrightarrow x\cdot\dfrac{7}{10}=\dfrac{2}{5}+\dfrac{5}{4}=\dfrac{8+25}{20}=\dfrac{33}{20}\)

\(\Leftrightarrow x=\dfrac{33}{20}:\dfrac{7}{10}=\dfrac{33}{20}\cdot\dfrac{10}{7}=\dfrac{33}{14}\)

c: \(\dfrac{7}{16}:\left(\dfrac{1}{4}x+\dfrac{9}{2}\right)-\dfrac{11}{6}=0\)

\(\Leftrightarrow\dfrac{7}{16}:\left(\dfrac{1}{4}x+\dfrac{9}{2}\right)=\dfrac{11}{6}\)

\(\Leftrightarrow x\cdot\dfrac{1}{4}+\dfrac{9}{2}=\dfrac{11}{6}:\dfrac{7}{16}=\dfrac{88}{21}\)

\(\Leftrightarrow x\cdot\dfrac{1}{4}=\dfrac{88}{21}-\dfrac{9}{2}=-\dfrac{13}{42}\)

hay \(x=-\dfrac{26}{21}\)

1: Ta có: \(\dfrac{-3}{x-4}-\dfrac{3-5x}{x^2-16}=\dfrac{1}{x+4}\)

Suy ra: \(-3\left(x+4\right)-3+5x=x-4\)

\(\Leftrightarrow-3x-12-3+5x-x+4=0\)

\(\Leftrightarrow x=11\left(nhận\right)\)

2. ĐKXĐ: $x\neq \pm 2$

PT \(\Leftrightarrow \frac{3(x-2)}{(2+x)(x-2)}-\frac{x-1}{(x-2)(x+2)}=\frac{2(x+2)}{(x-2)(x+2)}\)

\(\Leftrightarrow \frac{3(x-2)-(x-1)}{(x-2)(x+2)}=\frac{2(x+2)}{(x-2)(x+2)}\)

\(\Rightarrow 3(x-2)-(x-1)=2(x+2)\)

\(\Leftrightarrow 2x-5=2x+4\Leftrightarrow 9=0\) (vô lý)

Vậy pt vô nghiệm

3. ĐKXĐ: $x\neq \pm \frac{3}{2}$

PT \(\Leftrightarrow \frac{(x-5)(2x+3)-x(2x-3)}{(2x-3)(2x+3)}=\frac{1-6x}{(2x-3)(2x+3)}\)

\(\Rightarrow (x-5)(2x+3)-x(2x-3)=1-6x\)

\(\Leftrightarrow 2x^2-7x-15-2x^2+3x+6x-1=0\)

\(\Leftrightarrow 2x-16=0\Leftrightarrow x=8\) (thỏa mãn)

làm ơn giúp 🙏🙏🙏

a: =>1/3x+2/5x-2/5=0

=>11/15x-2/5=0

=>11/15x=2/5

=>x=2/5:11/15=2/5*15/11=30/55=6/11

b: =>-5x-1-1/2x+1/3=x

=>-11/2x-2/3-x=0

=>-13/2x=2/3

=>x=-2/3:13/2=-2/3*2/13=-4/39

c: (x+1/2)(2/3-2x)=0

=>x+1/2=0 hoặc 2/3-2x=0

=>x=1/3 hoặc x=-1/2

d: 9(3x+1)^2=16

=>(3x+1)^2=16/9

=>3x+1=4/3 hoặc 3x+1=-4/3

=>3x=1/3 hoặc 3x=-7/3

=>x=1/9 hoặc x=-7/9