Chứng minh Ax // Cy
NK
Những câu hỏi liên quan
mình rất muốn giúp bạn nhưng mình không có picturex10
Đúng 0
Bình luận (1)
Cho tam giác ABC cân tại A, có Am là đường trung tuyến. Vẽ tia Ax // BC. Vẽ tia Cy // AM, Ax cắt Cy tại I.
a/ Chứng minh AM vuông góc BC.
b/ Chứng minh AC = MI.
c/ Chứng minh ABMI là hình bình hành.
Giúp e vs ạ!

a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến ứng với cạnh đáy BC
nên AM là đường cao ứng với cạnh BC
b: Xét tứ giác AMCI có
AM//CI
AI//MC
Do đó: AMCI là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCI là hình chữ nhật
Suy ra: AC=MI
c: Ta có: AMCI là hình chữ nhật
nên AI=MC
mà MC=MB
nên AI=MB
Xét tứ giác ABMI có
AI//MB
AI=MB
Do đó: ABMI là hình bình hành
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A, có Am là đường trung tuyến. Vẽ tia Ax // BC. Vẽ tia Cy // AM, Ax cắt Cy tại I
a/ Chứng minh AM vuông góc BC
b/ Chứng minh AC = MI
c/ Chứng minh ABMI là hình bình hành
Giúp e vs ạ!
không cần vẽ hình
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến ứng với cạnh đáy BC
nên AM là đường cao ứng với cạnh BC
b: Xét tứ giác AMCI có
AI//MC
AM//CI
Do đó: AMCI là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCI là hình chữ nhật
hay AC=MI
c: Ta có: AICM là hình chữ nhật
nên AI=MC
mà MB=MC
nên AI=MB
Xét tứ giác AIMB có
AI//MB
AI=MB
Do đó: AIMB là hình bình hành
Đúng 1
Bình luận (0)
chứng minh Ax//Cy (song song)
Mình cần gấp ạ
cho tam giác abc từ a kẻ ax//bc từ c kẻ cy//ab tia ax cắt cy tại d
A)chứng minh abcd là hình bình hành
Cho tam giác ABC. Trên cùng một nửa mặt phẳng bờ là đg thẳng AC và không chứa điểm B vẽ hai tia Ax và Cy sao cho : Ax // BC ; Cy // BA và Ax cắt Cy tại D. Chứng minh : AB = CD và AD = BC
Vì Ax//BC
=>^xAC=^ACB(hai góc so le trong)
Vì Cy//BA
=>^BAC=^ACx(hai góc so le trong)
Xét ΔACB và ΔCAD có:
^ACB=^xAC(cmt)
AC:cạnh chung
^BAC=^ACx(cmt)
=>ΔACB=ΔCAD(g.c.g)
=>AB=CD(hai cạnh tương ứng)
=>AD=BC(hai cạnh tương ứng)
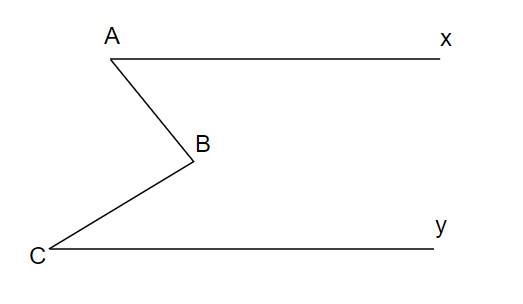
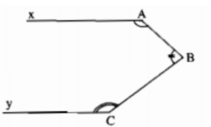
a) Cho Ax // Cy. So sánh góc ABC với góc A + góc C
b) Biết góc ABC = góc A + góc C . Chứng minh Ax // Cy
cho hình vẽ biết B=A+C chứng minh Ax // Cy
Kéo dài AB cắt Cy tại E và kéo dài CB cắt Ax tại G như hình vẽ dưới đây:
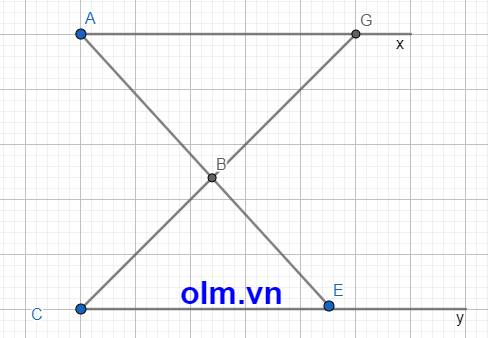
\(\widehat{ABC}\) = \(\widehat{GBE}\) (1) (vì đối đỉnh)
\(\widehat{GBE}\) = \(\widehat{BCE}\) + \(\widehat{CEB}\) (2) ( vì góc ngoài của tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{ABC}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\) (3)
Từ (1); (2); (3) ta có: \(\widehat{BCE}\) + \(\widehat{CEB}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\)
⇒ \(\widehat{CEB}\) = \(\widehat{GAB}\)
Mà hai góc CEB và góc GAB là hai góc ở vị trí so le trong nên
Cy // Ax (đpcm)
Đúng 1
Bình luận (0)
Hình dưới đây cho biết ∠A +∠B +∠C =360o. Chứng minh rằng Ax // Cy
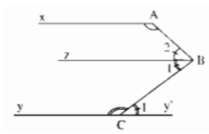
Kẻ Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ∠A +∠(B2 ) =180o
(2 góc trong cùng phía) (1)
Theo giả thiết ta có: ∠A +∠B + ∠C =360o (gt)
Hay ∠A +∠(B2 ) +∠(BCy) =360o (2)
Từ (1)và (2)suy ra :
∠(B1) + ∠BCy = 180o (3)
Lại có: ∠(C1 ) + ∠BCy =180o (hai góc kề bù) (4)
Từ (3) và (4) suy ra: ∠(B1 ) =∠(C1 )
Suy ra: Cy’ // Bz (vì có cặp góc so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra : Ax // Cy
Đúng 0
Bình luận (0)


