Mọi người ơi giúp mình với ạ. Từ câu 17 đến 27 ạ
Môi người ơi giúp mình câu 17 với ạ mình đang kiểm tra nên mọi người có kết quả share cho mình nhanh nha ạ
Mình nghĩ bạn nên tự làm bài kiểm tra nhé!
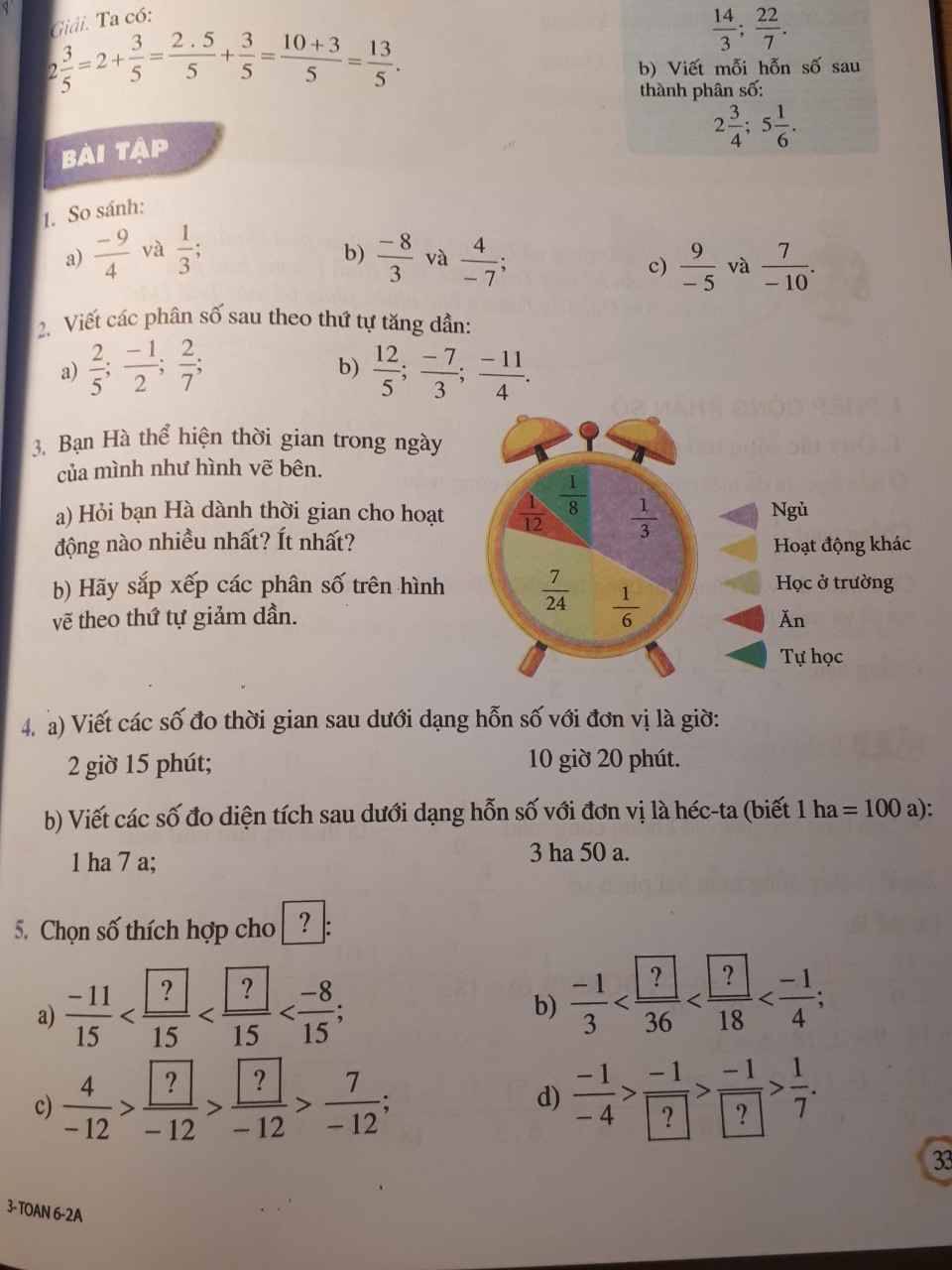 mọi người giúp mình từ câu 1 đến câu 5 với ạ
mọi người giúp mình từ câu 1 đến câu 5 với ạ
cảm ơn trước ạ
Câu 1:
a; \(\dfrac{-9}{4}\) < 0; \(\dfrac{1}{3}\) > o
\(\dfrac{-9}{4}\) < \(\dfrac{1}{3}\)
b; \(\dfrac{-8}{3}\) < - 1
\(\dfrac{4}{-7}\) > - 1
Vậy \(\dfrac{-8}{3}\) < \(\dfrac{4}{-7}\)
c; \(\dfrac{9}{-5}\) < - 1
\(\dfrac{7}{-10}\) > - 1
Vậy \(\dfrac{9}{-5}\) < \(\dfrac{7}{-10}\)
Câu 2:
a; Viết các phân số theo thứ tự tăng dần
\(\dfrac{-1}{2}\); \(\dfrac{2}{7}\); \(\dfrac{2}{5}\)
b; \(\dfrac{-11}{4}\); \(\dfrac{-7}{3}\); \(\dfrac{12}{5}\)
\(\dfrac{1}{3}\) = \(\dfrac{8}{24}\); \(\dfrac{1}{8}\) = \(\dfrac{3}{24}\); \(\dfrac{1}{6}\) = \(\dfrac{4}{24}\); \(\dfrac{1}{12}\) = \(\dfrac{2}{24}\); \(\dfrac{7}{24}\)
Hà giành thời gian nhiều nhất cho hoạt động Ngủ
Hà giành thời gian ít nhất cho hoạt động Ăn
Các phân số trong hình vẽ được sắp xếp theo thứ tự giảm dần là:
\(\dfrac{1}{3}\); \(\dfrac{7}{24}\); \(\dfrac{1}{6}\); \(\dfrac{1}{8}\); \(\dfrac{1}{12}\)
Mọi người ơi giúp mình 2 câu này với ạ. Mình cảm ơn mọi người rất nhiều ạ 
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
Mọi người ơi, giúp mình điền vào chỗ trống câu này với ạ. Cảm ơn mọi người ạ.

Mọi người ơi giúp mình làm câu 2 và câu 3 với ạ!! Mình xin cảm ơn rất nhiều ạ!
Từ câu 21 đến hết ạ. Mọi người giải giúp mình với, thankssss

mọi người ơi giúp mình câu này với ạ !!!!!!
giúp mình câu này với mọi người ơi .Mình cảm ơn ạ
2.
\(\Leftrightarrow cos2x-cos8x-sin3x+cos5x-2sin5x.cos5x=0\)
\(\Leftrightarrow2sin5x.sin3x-sin3x+cos5x-2sin5x.cos5x=0\)
\(\Leftrightarrow sin3x\left(2sin5x-1\right)-cos5x\left(2sin5x-1\right)=0\)
\(\Leftrightarrow\left(sin3x-cos5x\right)\left(2sin5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos5x=sin3x=cos\left(\dfrac{\pi}{2}-3x\right)\\sin5x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}-3x+k2\pi\\5x=3x-\dfrac{\pi}{2}+k2\pi\\5x=\dfrac{\pi}{6}+k2\pi\\5x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{16}+\dfrac{k\pi}{4}\\x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{30}+\dfrac{k2\pi}{5}\\x=\dfrac{\pi}{6}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
3.
\(\Leftrightarrow1+sinx=cosx-cos3x+2sinx.cosx+1-2sin^2x\)
\(\Leftrightarrow sinx=2sin2x.sinx+2sinx.cosx-2sin^2x\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\Rightarrow x=k\pi\\1=2sin2x+2cosx-2sinx\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow4sinx.cosx+2cosx-2sinx-1=0\)
\(\Leftrightarrow2cosx\left(2sinx+1\right)-\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2cosx+1\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)
4.
\(\Leftrightarrow2sin2x.cosx+sin2x=2cos2x.cosx+cos2x\)
\(\Leftrightarrow sin2x\left(2cosx+1\right)=cos2x\left(2cosx+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx+1=0\\sin2x=cos2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\tan2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{2\pi}{3}+k2\pi\\x=\dfrac{\pi}{8}+\dfrac{k\pi}{2}\\\end{matrix}\right.\)