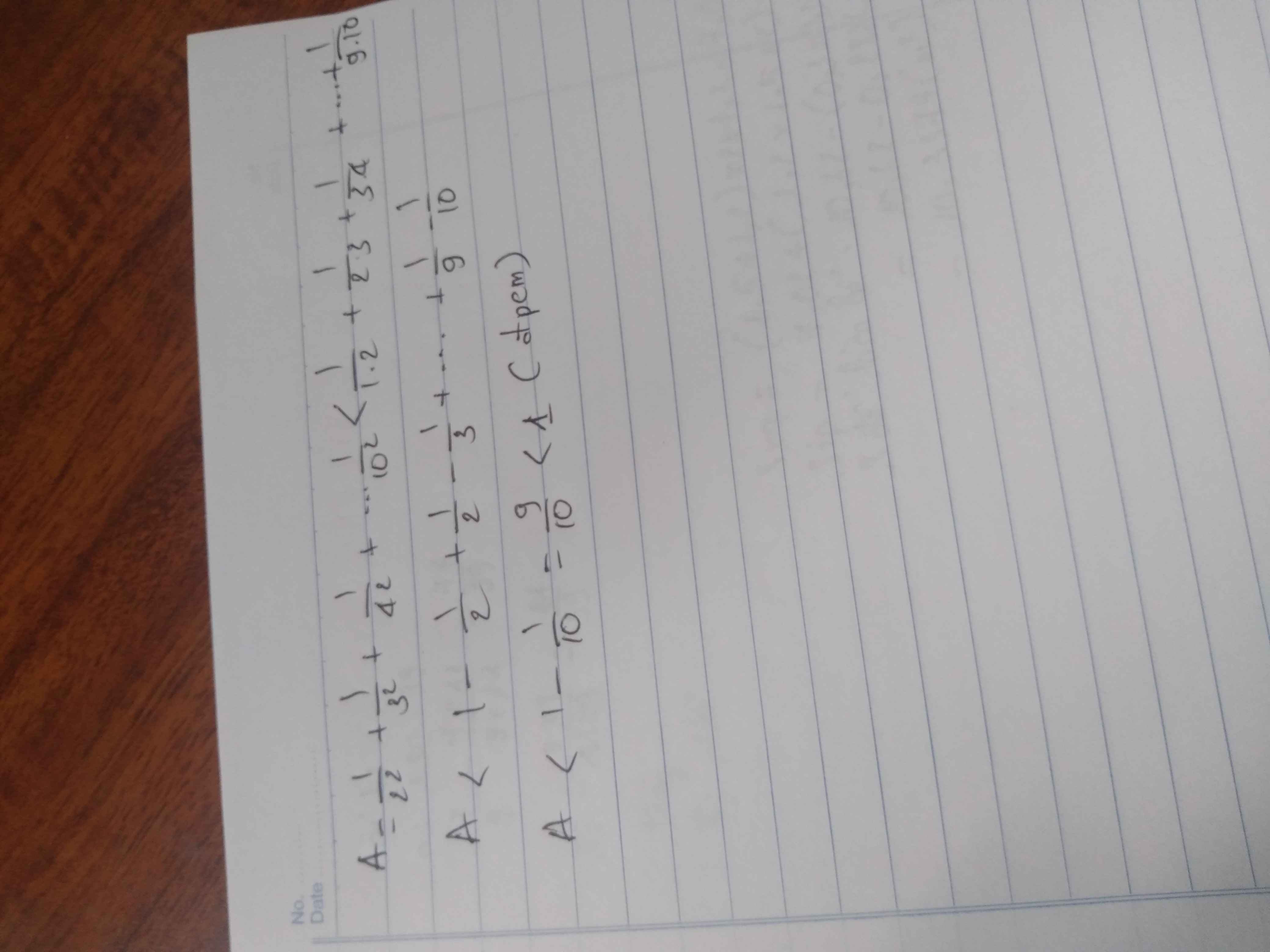Chứng minh rằng: S1=1-1/2^2-1/3^2-1/4^2-....- 1/10^2 > 0
DN
Những câu hỏi liên quan
Chứng minh rằng: S1=1-1/2^2-1/3^2-1/4^2-....- 1/10^2 > 0
S1 = 1-(1/2*2 + 1/3*3 + 1/4*4 +....+1/10*10)
Coi A = 1/2*2 +1/3*3 +1/4*4 +...+1/10*10
Ta thấy : 1/2*2 < 1/1*2
1/3*3 < 1/2*3
...1/10*10 < 1/9*10
=> A < 1/1*2 + 1/2*3 + 1/3*4 +...+1/9*10 = 9/10
=> 1 - A > 1 - 9/10
=> S1 > 1/10 > 0
Đúng 0
Bình luận (0)
Chứng minh rằng các tổng sau không phải số tự nhiên:
a) S1= 1/2+1/3+1/4
b) S2= 1/2+1/3+1/4+...+1/8
c) S3= 1/2+1/3+...+1/16
d) S4= 3/10+3/11+..+3/14
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 0Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| |a + b|Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| |a − b|Bài 8. Chứng minh rằng: |x − 1| + |x − 2| 1Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| 2Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| 4Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| 2
Đọc tiếp
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 =0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| < |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 0Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| |a + b|Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|Bài 8. Chứng minh rằng: |x − 1| + |x − 2| 1Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| 2Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| 4Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| 2
Đọc tiếp
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)
2 = 0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
Bài 1: Tính tổng
a) S1 = 1 - 2 + 3 - 4 +...+ 1997 - 1998 + 1999
b) S2 = 1 - 4 + 7 - 10 +...-2998 + 3001
Bài 2: Chứng minh rằng nếu 6x + 11y chia hết cho 31 thì x + 7y cũng chia hết cho 31
a) S1 = 1 - 2 + 3 - 4 + ... + 1997 - 1998 + 1999
=> S1 = (-1) + (-1) + (-1) + ... + (-1) + 1999
=> S1 = (-999) + 1999
=> S1 = 1000
Đúng 0
Bình luận (0)
Ta có S1 = (1 - 2) + (3 - 4) + ....... + (1997 - 1998) + 1999
= -1 + -1 + -1 + ..... + -1 + 1999
= -999 + 1999
=1000
Đúng 0
Bình luận (0)
1.S1 = 1 - 2 + 3 - 4 + ... + 1997 - 1998 + 1999
= (1-2) + (3-4)+...+(1997-1998)+1999
= - 1 + -1 + ...+ -1 + 1999
SH : 1998 - 1 +1
=1998
= 1998 : 2
= 999
TDS: -1 . 999
= -999 + 1999
= 1000
b.S2 = 1 - 4 + 7 - 10 + ... - 2998 + 3001
= (1 - 4) +(7 -10) + ...+(2995 - 2998) + 3001
= -3 + -3 + -3 +...+ -3 + 3001
SH=(2998 - 1) : 3 + 1
= 1000
= 1000 : 2
= 500
= 500 . -3
= -1500 + 3001
= 1501
bài 2 mình ko piết làm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 2 : Chứng minh rằng
a) 2^0 + 2^1 + 2^2 + 2^3 + 2^4 ko chia hết cho 3
b) 8^0 + 8^1 + ... + 8^9 + 8^10 ko chia hết cho 9
1) Tính: A 2/4.7-3/5.9+2/7.10-3/9.13+..+2/301.304-3/401.4052) Chứng minh rằng với mọi n thuộc số tự nhiên, n lớn hơn hoặc bằng 2: 3/9.14+3/14.19+...+3/(5n-1).(5n+4)1/153) a) Cho A9/5^2+9/11^2+9/17^2+...+9/305^2. Chứng minh A3/4b) Cho C4/3+7/3^2+10/3^3+...+3n+1/3^n với số tự nhiên khác 0. Chứng minh rằng C11/44) Tính: a) 1/2+1/2^2+1/2^3+...+1/2^100b) B1/3-1/3^2+1/3^3-1/3^4+...+1/3^99-1/3^1005) So sánh: (1-1/2).(1-1/3).(1-1/4). ... .(1-1/20) với 1/21
Đọc tiếp
1) Tính: A= 2/4.7-3/5.9+2/7.10-3/9.13+..+2/301.304-3/401.405
2) Chứng minh rằng với mọi n thuộc số tự nhiên, n lớn hơn hoặc bằng 2: 3/9.14+3/14.19+...+3/(5n-1).(5n+4)<1/15
3) a) Cho A=9/5^2+9/11^2+9/17^2+...+9/305^2. Chứng minh A<3/4
b) Cho C=4/3+7/3^2+10/3^3+...+3n+1/3^n với số tự nhiên khác 0. Chứng minh rằng C<11/4
4) Tính: a) =1/2+1/2^2+1/2^3+...+1/2^100
b) B=1/3-1/3^2+1/3^3-1/3^4+...+1/3^99-1/3^100
5) So sánh: (1-1/2).(1-1/3).(1-1/4). ... .(1-1/20) với 1/21
chứng minh rằng : 1-1/2 - 1/2^2 - 1/ 2^3 - 1/2^4 - ...............-1/2^10 > 1/2^11
\(\Leftrightarrow2-\left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{11}}\right)>0\)
Ta có: \(\frac{1}{2^{12}}-1=\left(\frac{1}{2}-1\right)\left(\frac{1}{2^{11}}+\frac{1}{2^{10}}+\frac{1}{2^9}+...+\frac{1}{2}+1\right)\)
\(\Rightarrow1+\frac{1}{2}+...+\frac{1}{2^{11}}=2\left(1-\frac{1}{2^{12}}\right)=2-\frac{1}{2^{11}}\)
\(\Rightarrow2-\left(1+\frac{1}{2}+...+\frac{1}{2^{11}}\right)=2-\left(2-\frac{1}{2^{11}}\right)=\frac{1}{2^{11}}>0\left(đpcm\right)\)
Đúng 0
Bình luận (0)
1-1/2-1/2^2-......-1/2^11
ta có:1-1/2-1/2^2-.....-1/2^11=1-(1/2+1/2^2+....+1/2^11)
A=1/2+1/2^2+1/2^3+...+1/2^11
2A=2.(1/2+1/2^2+1/2^3+...+1/2^11)
2A=2.1/2+2.1/2^2+....+2.1/2^11
2A-A=(1+1/2^2+1/2^3+...+1/2^10)-(1/2+1/2^2+1/2^3+....+1/2^11)
A=1-1/2^11=2048/2048-1/2048=2047/2048
vì 1-(1/2+1/2^2+1/2^3+...+1/2^11)=1-A
=> 1-(1/2+1/2^2+1/2^3+...+1/2^11)=1-2047/2048=2048/2048-2047/2048=1/2048=1/2^11
vậy 1-1/2-1/2^2-1/2^3-...-1/2^11=1/2^11
Đúng 0
Bình luận (0)
Chứng minh rằng \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{10^2}< 1\)
Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{10^2}< \dfrac{1}{9.10}\)
cộng vế với vê sta đc
\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}=1-\dfrac{1}{10}=\dfrac{9}{10}< 1\)
Vậy ta có đpcm
Đúng 1
Bình luận (0)