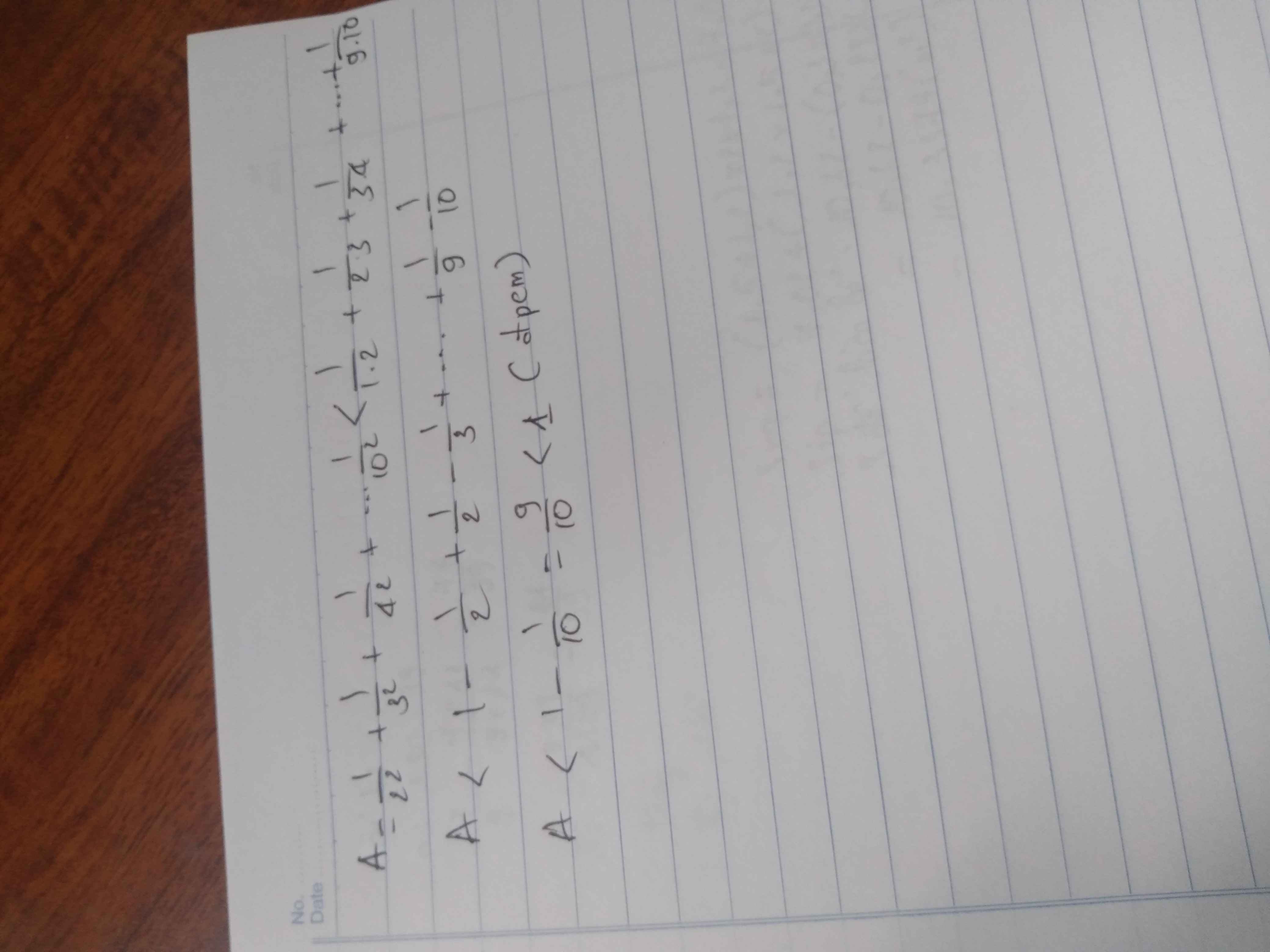Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{10^2}< \dfrac{1}{9.10}\)
cộng vế với vê sta đc
\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}=1-\dfrac{1}{10}=\dfrac{9}{10}< 1\)
Vậy ta có đpcm