cái nay chịu

CHÚC BẠN HỌC GIỎI

TK MÌNH NHÉ

minh biết rồi BEC = 90^o nhé đảm bảo đúng 

CHÚC BẠN HỌC GIỎI

TK MÌNH NHÉ

Giúp với

HÌnh bn tự vẽ nha

Kẻ đường cao DE

=> CE=10

=> tam giác BCE vuông cân tại E

=> góc EBC=45 độ

=> ABC=45+90=135 độ

a) có : 2AD=2CD =>AD=CD

^A=^D=^AHC=90 độ =>hình vuông AHCD =>AH=HC=AD

Mà AB = 2AD =>tam giác ABC vuông tại C

tam giác ACD vuông cân tại D => ^ACD=45 độ =>^BCD=135 độ

Mà ^BCD + ^B = 180 độ => ^B = 45 độ

hình thang.

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)

\(AC=a\sqrt{2}\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{\sqrt{3}}{3}\)

\(\Rightarrow\widehat{SCA}=30^0\)

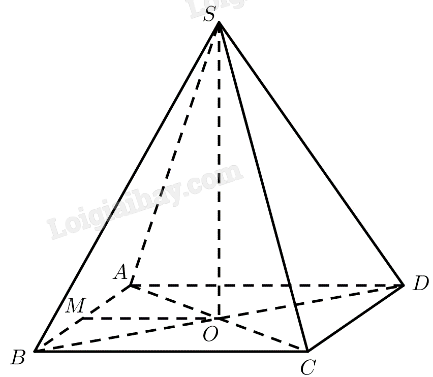
a) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)

Tam giác \(SAC\) là tam giác đều \( \Rightarrow \widehat {SAO} = {60^ \circ }\)

\( \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = {60^ \circ }\)

b) \(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)

\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)

\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right)\)

\( \Rightarrow \left( {SA,\left( {SB{\rm{D}}} \right)} \right) = \left( {SA,SO} \right) = \widehat {ASO} = \frac{1}{2}\widehat {ASC} = {30^ \circ }\)

c) \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot MO,SO \bot DO\)

Vậy \(\widehat {MO{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {M,SO,D} \right]\)

\(ABCD\) là hình vuông \(\widehat {AOD} = {90^ \circ }\)

\(\Delta AMO\) vuông cân tại \(M \Rightarrow \widehat {AOM} = {45^ \circ }\)

\( \Rightarrow \widehat {MO{\rm{D}}} = \widehat {AOM} + \widehat {AO{\rm{D}}} = {45^ \circ } + {90^ \circ } = {135^ \circ }\)

Vậy số đo của góc nhị diện \(\left[ {M,SO,D} \right]\) bằng \({135^ \circ }\).

Có 1 phần tư quả táo hỏi xem có bao nhiêu quả táo và số đó là 54