Các bạn chỉ mình : ví dụ căn 45a . Căn 2a -4a chẳng hạn khi mà giải ra với a
MT
Những câu hỏi liên quan
Các bạn chỉ mình : Ví dụ căn 45a . Căn 4a -5a chẳng hạn khi mà a <0 thì chỉ đổi dấu ở chỗ giá trị tuyệt đối thôi ạ còn cái a mà ko nằm trong trị tuyệt đối thì không đỏi dấu ạ
Các bạn ơi Cho mình hỏi khi mà tìm điều kiện trong giá trị tuyệt đối để xem xem số trong giá trị tuyệt đối là âm hay là dương thì chỉ lấy nhưng cái có căn dạng căn (A^2) |A| thôi ạ còn. Ví dụ Căn (5a) . Căn (45a) -3a thig chỉ tìm điều kiện ở chỗ căn (225a^2) ( vì nó có trị tuyệt đối) còn những con a đứng 1 mình hoặc cùng với số khác thì nó có cần đổi dấu khi mà trong trị tuyệt đối là a
Đọc tiếp
Các bạn ơi Cho mình hỏi khi mà tìm điều kiện trong giá trị tuyệt đối để xem xem số trong giá trị tuyệt đối là âm hay là dương thì chỉ lấy nhưng cái có căn dạng căn (A^2) =|A| thôi ạ còn. Ví dụ Căn (5a) . Căn (45a) -3a thig chỉ tìm điều kiện ở chỗ căn (225a^2) ( vì nó có trị tuyệt đối) còn những con a đứng 1 mình hoặc cùng với số khác thì nó có cần đổi dấu khi mà trong trị tuyệt đối là a
Không cần đổi dấu giá trị tuyệt đối
Đúng 0
Bình luận (0)
Cách hỏi của bạn thực sự hơi khó hiểu. Mình chỉ trả lời theo cách hiểu của mình về câu hỏi của bạn thôi nhé.
- Thứ nhất, không cần phải tìm điều kiện của số trong giá trị tuyệt đối. Thông thường khi đến đoạn $\sqrt{a^2}=|a|$ thì đề bài đã có sẵn điều kiện $a\geq 0$ hoặc $a< 0$ để bạn tiếp tục thực hiện đến đoạn phá trị tuyệt đối. Ví dụ, cho $a< 0$ thì $\sqrt{a^2}=|a|=-a$
- Thứ hai, trong trường hợp $\sqrt{5a}.\sqrt{45a}-3a$, điều kiện để biểu thức này có nghĩa là $5a\geq 0$ và $45a\geq 0$, hay $a\geq 0$.
Khi đó, để phá căn và xuất hiện trị tuyệt đối, bạn thực hiện $\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\sqrt{(15a)^2}-3a=|15a|-3a=15a-3a=12a$
Đúng 1
Bình luận (0)
Các bạn ơi Cho mình hỏi khi mà tìm điều kiện trong giá trị tuyệt đối để xem xem số trong giá trị tuyệt đối là âm hay là dương thì chỉ lấy nhưng cái có căn dạng căn (A^2) |A| thôi ạ còn. Ví dụ
Căn (5a) . Căn (45a) -3a thig chỉ tìm điều kiện ở chỗ căn (225a^2) ( vì nó có trị tuyệt đối) còn những con a đứng 1 mình hoặc cùng với số khác thì nó có cần đổi dấu khi mà trong trị tuyệt đối là a
Đọc tiếp
Các bạn ơi Cho mình hỏi khi mà tìm điều kiện trong giá trị tuyệt đối để xem xem số trong giá trị tuyệt đối là âm hay là dương thì chỉ lấy nhưng cái có căn dạng căn (A^2) =|A| thôi ạ còn. Ví dụ Căn (5a) . Căn (45a) -3a thig chỉ tìm điều kiện ở chỗ căn (225a^2) ( vì nó có trị tuyệt đối) còn những con a đứng 1 mình hoặc cùng với số khác thì nó có cần đổi dấu khi mà trong trị tuyệt đối là a
Các bạn ơi Ví dụ căn (16x) =căn (81) . Khi mà làm mất căn đi theo ý hiểu của mình là bình phương hai vế lên để mất căn ( vì hai vế bằng nhau rồi và cùng bình phương lên thì nó cũng vẫn bằng nhau ) . Mình có đúng không ạ. Nếu mà sai thì các bạn chỉ ra lỗi sai giúp mình và giải thích rõ hộ giúp mình ạ
\(\sqrt{f\left(x\right)}=\sqrt{g\left(x\right)}\left(ĐK:\left[{}\begin{matrix}f\left(x\right)\ge0\\g\left(x\right)\ge0\end{matrix}\right.\right)\\ \Leftrightarrow f\left(x\right)=g\left(x\right)\)
Trong ví dụ \(\sqrt{16x}=\sqrt{81}\), trước khi bình phương 2 vế để phá dấu căn thì bạn cần ghi điều kiện \(16x\ge0\Leftrightarrow x\ge0\) nhé.
Đúng 1
Bình luận (5)
\(\sqrt{16x}=\sqrt{81}\left(ĐK:x\ge0\right)\\ \Leftrightarrow\left(\sqrt{16x}\right)^2=\left(\sqrt{81}\right)^2\\ \Leftrightarrow16x=81\\ \Leftrightarrow x=\dfrac{81}{16}\left(tmđk\right)\)
Thử lại: \(\sqrt{16.\dfrac{81}{16}}=\sqrt{81}\\ \Leftrightarrow\sqrt{81}=\sqrt{81}\left(\text{luôn đúng}\right)\)
Đúng 0
Bình luận (3)
Các bạn chỉ mình Căn bậc hai hai số học thì luôn không âm là cái số trong căn hay là cả căn ạ Ví dụ tìm x căn x =-3
Phân tích rõ một chút nhé :
- Căn bậc 2 của số x (bắt buộc là số x phải >=0 ) là \(\sqrt{x},-\sqrt{x}\)
Thì căn bậc 2 số học của x là \(\sqrt{x}\)(do\(\sqrt{x}\ge0\))
- Đối với trường hợp căn bậc 2 số học của x2 thì là |x|
Đúng 0
Bình luận (5)
Chắc chắn là cả căn rồi bạn
Đúng 0
Bình luận (0)
Các Bạn không cần làm mà chỉ mình chỗ này mình chưa hiểu :
Phần B Khi mà giải ra B = 4/( 3 - căn x) thì làm sao để biết được (3 - căn x) này là âm ạ. Hay cả trên tử cũng vậy (1+căn x) 
\(3-\sqrt{x}\) chưa chắc đã âm
thử x=4=>3-2=1>0
Đúng 0
Bình luận (1)
Các bạn chỉ cho mình:
+ Tại sao không giải ra từng cái là P và căn P rồi so sánh. Chỉ mình tại sao lại không làm được, với nếu mà đề ra như nào thì có thể giải ra từng cái 1 P và căn P
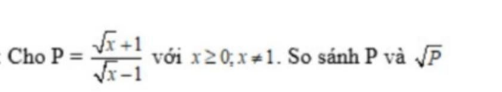
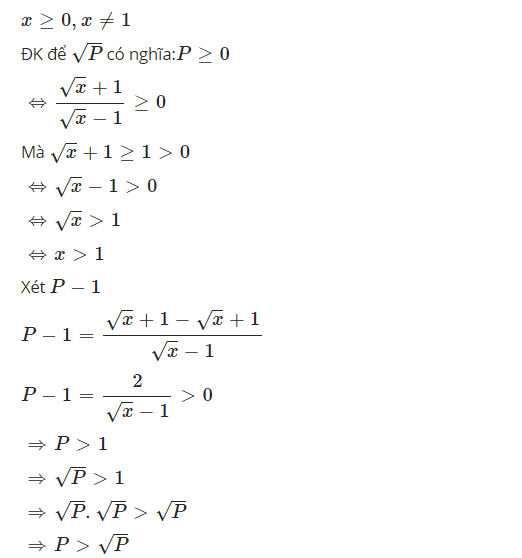
Tại sao không giải ra $\sqrt{P}$ và $\sqrt{P}$?
Em đã có $P$ rồi, nhưng với $\sqrt{P}$, em làm sao rút gọn được khi mà $P$ đã khá gọn rồi. Cũng chẳng có giá trị nào của $x$ để tính cụ thể $P, \sqrt{P}$ rồi đi so sánh. Vì vậy cách này không khả thi.
Vậy thì phải tìm hướng khác. Muốn so sánh 2 số, ta xét hiệu hai số đó.
$P-\sqrt{P}=\sqrt{P}(\sqrt{P}-1)$
Rõ ràng $\sqrt{P}$ đã dương rồi, giờ ta phải xem xét xem $\sqrt{P}-1$ âm hay dương, hay $P$ có lớn hơn 1 không
Đó là lý do vì sao bài giải như trên.
Đúng 1
Bình luận (5)
Còn câu hỏi khi nào giải ra từng cái $P$ và $\sqrt{P}$, thì đó là khi đề cho $x=2$ chả hạn, so sánh $P$ và $\sqrt{P}$.
Nhưg hầu như sẽ chẳng có đề nào ra kiểu vậy, mà đa số lợi dụng tính chất của phân thức đó để so sánh (ví dụ như trong bài tính chất nổi bật là $P>1$) cho nhanh. Đó là cái hay của đề bài.
Đúng 1
Bình luận (0)
Các Bạn không cần làm mà chỉ mình chỗ này mình chưa hiểu : Phần B Khi mà giải ra B = 4/( 3 - căn x) thì làm sao để biết được (3 - căn x) này là âm ạ. Hay cả trên tử cũng vậy (1+căn x) ( liên quan tới hình ảnh bên dưới) 
cái này thì ko nhất thiết phải Cm nha bạn
Câu b kêu tìm x để B ko nhỏ hơn hoặc bằng A
Nghĩa là
\(\dfrac{4}{3-\sqrt{x}}>1\)
\(\Leftrightarrow\dfrac{4}{3-\sqrt{x}}-1>0\)
\(\Leftrightarrow\dfrac{4-\left(3-\sqrt{x}\right)}{3-\sqrt{x}}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{3-\sqrt{x}}>0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}+1>0\\3-\sqrt{x}>0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}+1< 0\left(VL\right)\\3-\sqrt{x}< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 3\)
\(\Leftrightarrow x< 9\)
Theo Đk ta có x≥0
Vậy 0≤x<9 thì B ko nhỏ hơn hoặc bằng A
Đúng 1
Bình luận (1)
Lời giải giống như bạn dưới đã viết.
Để $B$ không nhỏ hơn hoặc bằng $A$
Tức là $B>A$
$\Leftrightarrow \frac{4}{3-\sqrt{x}}>1$
$\Leftrightarrow \frac{4}{3-\sqrt{x}}-1>0\Leftrightarrow \frac{\sqrt{x}+1}{3-\sqrt{x}}>0$
Để phân thức này dương thì tử và mẫu phải cùng dấu.
Mà $\sqrt{x}+1\geq 0+1>0$ (dương rồi) nên $\sqrt{3}-x$ cũng dương.
------------------------
Đây là cách dễ làm nhất đối với bài này.
------------------------
Về phần lời giải của cô em, chị nghĩ trong lúc giảng em bị miss mất 1 số ý chứ ý cô không phải khẳng định mẫu âm đâu. Có lẽ ý của cô em thế này:
Khi em có: $\frac{4}{3-\sqrt{x}}>1$ thì em không nên nhân chéo mà nên trừ để đưa về hiệu >0 (như bạn Khoa đã giải). Nếu nhân chéo, em sẽ mắc phải 2 TH mẫu âm, mẫu dương như sau:
TH1: $3-\sqrt{x}>0$ thì $\frac{4}{3-\sqrt{x}}>1$ tương đương với $4> 3-\sqrt{x}$
TH2: $3-\sqrt{x}< 0$ thì tương đương $4< 3-\sqrt{x}$ (khi nhân 2 vế với số âm thì phải đổi dấu)
Như vậy thì rất là phức tạp. Nên để tránh TH mẫu âm mà hs giữ nguyên dấu khi nhân chéo thì cô em khuyên như vậy.
Đúng 0
Bình luận (0)
Em còn chỗ nào chưa hiểu thì cứ hỏi thoải mái.
Đúng 0
Bình luận (0)
Các bạn ơi chỉ mình : Ví dụ như trong căn phải là số không âm ví dụ như căn (x-1) thì lúc nào x cũng luôn lớn hơn hoặc bằng 0 rồi nhưng sao phải lấy cả x-1 >=0 ạ
Đề ví dụTimf x không âm biết căn (x-1)=...... Đề bải x không âm thì chỉ cần x>=0 thôi chứ ạ. Chỉ rõ chio mình hiểu nhá
Đúng 0
Bình luận (0)
Vì khi lấy ĐKXĐ thì lấy cả biểu thức trong căn mới đúng
Đúng 0
Bình luận (0)





