TH1: x + y + z $\ne$ 0

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{y+z+1}$ = $\frac{y}{x+z+2}$ = $\frac{z}{x+y-3}$ = $\frac{x+y+z}{y+z+1+x+z+2+x+y-3}$ 

              = $\frac{x+y+z}{x+y+z+x+y+z}$ = $\frac{x+y+z}{2(x+y+z)}$ = $\frac{1}{2}$ 

⇒ x + y + z = $\frac{1}{2}$

⇒ x + y       = $\frac{1}{2}$ - z

    x + z        = $\frac{1}{2}$ - y

    y + z        = $\frac{1}{2}$ - x

Thay y + z + 1 = 

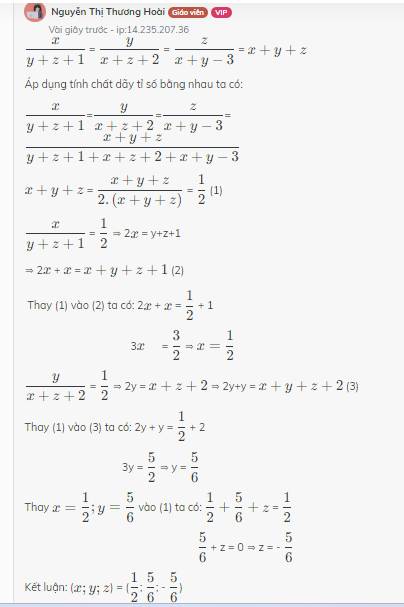
https://olm.vn/cau-hoi/tim-tat-ca-cac-so-xyz-biet-dfracxyz1dfracyxz2dfraczxy-3xyz-giair-chi-tiet-ho-e-vs-a.8297156371934

số lớn 405:(5+4).5=225

số bé 405-225=180

sai rồi bạn ơi

bn ơi đề bài sai r mik tíh ko ra

Câu 5 đáng lẽ phải có điều kiện gì mới được chứ.

VD

a=2,

b=c=d=e=g=1

Thấy vào thì 9≥10 là vô lí

  36 x ( 10 + 1 )

= 36 x 11

= 396

  36 x 10 + 36 x 1

= 360 + 36

= 396

Cách 1 :

36 x ( 10 + 1 )

= 36 x 11

= 396

Cách 2 :

36 x ( 10 + 1 )

= 36 x 10 + 36 x 1

= 360 + 36 

= 396

cách 1 :

36 x (10+1)

=36 x 11

= 396

cách 2:

36 x (10+1)

=(36 x 10) +( 36 x 1)

= 360         +      36

= 396

 k cho mik nha 

gợi ý nè:

thử cộng chúng lại xem

\(\dfrac{x}{y+z+1}\) = \(\dfrac{y}{x+z+2}\) = \(\dfrac{z}{x+y-3}\) = \(x+y+z\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{y+z+1}\)=\(\dfrac{y}{x+z+2}\)=\(\dfrac{z}{x+y-3}\)=\(\dfrac{x+y+z}{y+z+1+x+z+2+x+y-3}\)

\(x+y+z\) = \(\dfrac{x+y+z}{2.\left(x+y+z\right)}\) = \(\dfrac{1}{2}\) (1)

\(\dfrac{x}{y+z+1}\) = \(\dfrac{1}{2}\) ⇒ 2\(x\) = y+z+1 

⇒ 2\(x\) + \(x\) = \(x+y+z+1\) (2)

 Thay (1) vào (2) ta có: 2\(x\) + \(x\) = \(\dfrac{1}{2}\) + 1

                                      3\(x\)      = \(\dfrac{3}{2}\) ⇒ \(x=\dfrac{1}{2}\)

\(\dfrac{y}{x+z+2}\) = \(\dfrac{1}{2}\) ⇒ 2y = \(x+z+2\) ⇒ 2y+y = \(x+y+z+2\) (3)

Thay (1) vào (3) ta có: 2y + y = \(\dfrac{1}{2}\) + 2 

                                   3y = \(\dfrac{5}{2}\) ⇒ y = \(\dfrac{5}{6}\)

Thay \(x=\dfrac{1}{2};y=\dfrac{5}{6}\) vào (1) ta có: \(\dfrac{1}{2}+\dfrac{5}{6}+z\) = \(\dfrac{1}{2}\)

                                                              \(\dfrac{5}{6}\) + z = 0 ⇒ z = - \(\dfrac{5}{6}\)

Kết luận: (\(x;y;z\)) = (\(\dfrac{1}{2}\); \(\dfrac{5}{6}\); - \(\dfrac{5}{6}\))

Câu 2:

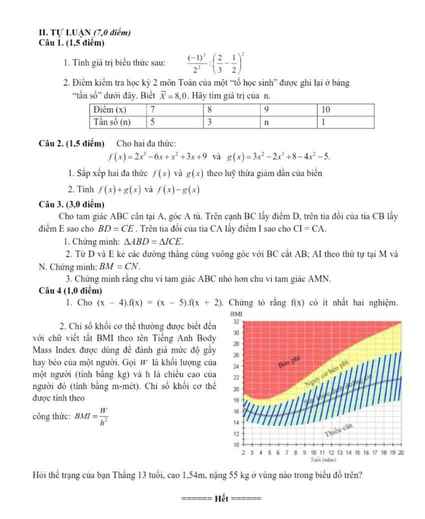
\(1.f\left(x\right)=2x^3+x^2-3x+9.\\ g\left(x\right)=-2x^3-x^2+3.\)

Câu 3:

1. Ta có: \(AB=AC\) (\(\Delta ABC\) cân).

Mà \(AC=IC\left(gt\right). \)

\(\Rightarrow AB=IC.\)

Ta có: \(\widehat{ABC}=\widehat{ACB}\) (\(\Delta ABC\) cân).

Mà \(\widehat{ACB}=\widehat{ICE}\) (đối đỉnh).

\(\Rightarrow\widehat{ABC}=\widehat{ICE}.\)

Hay \(\widehat{ABD}=\widehat{ICE}.\)

Xét \(\Delta ABD\) và \(\Delta ICE:\)

BD = CE (gt).

\(\widehat{ABD}=\widehat{ICE}\left(cmt\right).\)

AB = IC (cmt).

\(\Rightarrow\Delta ABD=\Delta ICE\left(c-g-c\right).\)

2. Xét \(\Delta BDM\) và \(\Delta CEN:\)

\(\widehat{MBD}=\widehat{NCE}\left(\widehat{ABD}=\widehat{ICE}\right).\)

\(BD=CE\left(gt\right).\)

\(\widehat{BDM}=\widehat{CEN}\left(=90^o\right).\)

\(\Rightarrow\Delta BDM=\Delta CEN\left(g-c-g\right).\)

\(\Rightarrow BM=CN\) (2 cạnh tương ứng).

My mother's a professional clerk in Clingme company. She's quite strict, but sometimes humorous and kind. She's definitely the best cook in the family, and I ...( like hoặc love ) her.

\(6,\\ a,P=9\left(x^2-2\cdot\dfrac{1}{9}x+\dfrac{1}{81}\right)+\dfrac{26}{9}=9\left(x-\dfrac{1}{9}\right)^2+\dfrac{26}{9}\ge\dfrac{26}{9}\\ P_{min}=\dfrac{26}{9}\Leftrightarrow x-\dfrac{1}{9}=0\Leftrightarrow x=\dfrac{1}{9}\\ b,Q=3\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\\ Q_{min}=\dfrac{1}{4}\Leftrightarrow x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\\ c,R=\left(x^2-2xy+y^2\right)+x^2+1=\left(x-y\right)^2+x^2+1\ge1\\ R_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x-y=0\\x=0\end{matrix}\right.\Leftrightarrow x=y=0\)