Làm topic : Introduce one of heritage sites in Vietnam Giúp mk với 😓😓😓
HN
Những câu hỏi liên quan
Giúp mk câu 16,17 ,18 với ạ 😓😓😓😓😓😞
Câu 16.
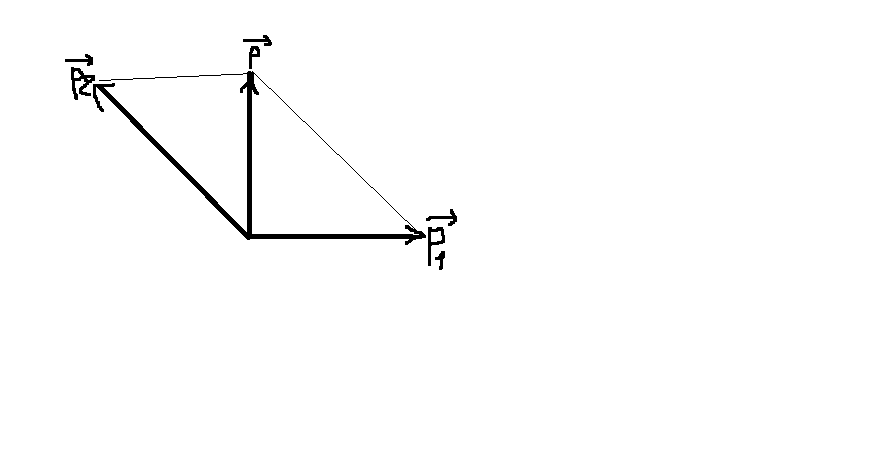
Hình vẽ tương đối thôi nha!!!
Bảo toàn động lương ta có:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
\(\Rightarrow p^2=p_2^2-p_1^2\)\(\Rightarrow p_2=\sqrt{p^2+p_1^2}\)
\(\Rightarrow m_2\cdot v_2=\sqrt{\left(m_1+m_2\right)\cdot v+m_1\cdot v_1}\)
\(\Rightarrow0,3\cdot v_2=\sqrt{[\left(0,5+0,3\right)\cdot3]^2+(0,5\cdot4)^2}=3,124\)
\(\Rightarrow v_2=10,41\)m/s
Đúng 3
Bình luận (0)
Xin phép đã làm phiền. Giúp mình với mn 😓😓😓
Theo giả thiết, ta có:
\left( {\widehat {SC,\left( {ABC} \right)}} \right) = \widehat {SCA} = {30^^\circ } \Rightarrow SA = AC\tan {30^^\circ } = \frac{{a\sqrt 3 }}{3}
Vậy thể tích khối chóp S.ABC là:
Đúng 0
Bình luận (0)
Giúp em câu b bài 1 với ạ😓😓😓😓😓😓
Phương trình hoành độ giao điểm (d) và (P):
\(x^2-2x-3=ax-a-3\)
\(\Leftrightarrow x^2-\left(a+2\right)x+a=0\)
\(\Delta=\left(a+2\right)^2-4a=a^2+4>0;\forall a\Rightarrow\) (d) luôn cắt (P) tại 2 điểm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=a+2\\x_Ax_B=a\end{matrix}\right.\)
Mặt khác do A, B thuộc (d) nên: \(\left\{{}\begin{matrix}y_A=ax_A-a-3\\y_B=ax_B-a-3\end{matrix}\right.\)
\(y_A+y_B=0\)
\(\Leftrightarrow a\left(x_A+x_B\right)-2a-6=0\)
\(\Leftrightarrow a\left(a+2\right)-2a-6=0\)
\(\Leftrightarrow a^2-6=0\)
\(\Leftrightarrow a=\pm\sqrt{6}\)
Đúng 0
Bình luận (0)
Giúp mình với mn ơi 😓😓😓 nếu đc có thể ghi giúp mình tự chọn là từ loại j với 😓😓😓
1A(adj)
2D(n)
3A(adj)
4C(n)
5D(adj)
6C(adj)
7B(n)(Tham khảo c7)
8A(n)
9C(n)
10B(v)
11A(adv)
Đúng 2
Bình luận (2)
Giúp em bài 2 với😓😓😓
\(\dfrac{x-3}{3x-5}< \dfrac{3x-5}{x-3}.\left(x\ne3;x\ne\dfrac{5}{3}\right).\)
\(\Leftrightarrow\dfrac{x-3}{3x-5}-\dfrac{3x-5}{x-3}< 0.\Leftrightarrow\dfrac{\left(x-3\right)^2-\left(3x-5\right)^2}{\left(3x-5\right)\left(x-3\right)}< 0.\)
\(\Leftrightarrow\dfrac{x^2-6x+9-\left(9x^2-30x+25\right)}{\left(3x-5\right)\left(x-3\right)}< 0.\) \(\Leftrightarrow\dfrac{x^2-6x+9-9x^2+30x-25}{\left(3x-5\right)\left(x-3\right)}< 0.\)
\(\Leftrightarrow\dfrac{-8x^2+24x-16}{\left(3x-5\right)\left(x-3\right)}< 0.\Leftrightarrow\dfrac{8x^2-24x+16}{\left(3x-5\right)\left(x-3\right)}>0.\)
\(\Leftrightarrow\dfrac{8\left(x^2-3x+2\right)}{\left(3x-5\right)\left(x-3\right)}>0.\Leftrightarrow\dfrac{\left(x-2\right)\left(x-1\right)}{\left(3x-5\right)\left(x-3\right)}>0.\)
Đặt \(\dfrac{\left(x-2\right)\left(x-1\right)}{\left(3x-5\right)\left(x-3\right)}=f\left(x\right).\)
Lập bảng xét dấu:
| x | \(-\infty\) 1 \(\dfrac{5}{3}\) 2 3 \(+\infty\) |
| x - 2 | - | - | - 0 + | + |
| x - 1 | - 0 + | + | + | + |
| 3x - 5 | - | - 0 + | + | + |
| x - 3 | - | - | - | - 0 + |
| f (x) | + 0 - || + 0 - || + |
Vậy \(\dfrac{\left(x-2\right)\left(x-1\right)}{\left(3x-5\right)\left(x-3\right)}=f\left(x\right)>0.\) \(\Leftrightarrow x\in\left(-\infty;1\right)\cup\left(\dfrac{5}{3};2\right)\cup\left(3;+\infty\right).\)
Đúng 1
Bình luận (0)
a)
\(\left\{{}\begin{matrix}2x^2+7x-4\ge x^2-4\\\dfrac{2x-1}{x^2+x-2}< \dfrac{2x-5}{x^2+x-2}\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x^2+7\ge0\\\dfrac{2x-5-2x+1}{x^2+x-2}>0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x\left(x+7\right)\ge0\\\dfrac{-4}{x^2+x-2}>0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x\left(x+7\right)\ge0\\\left(x-1\right)\left(x+2\right)< 0\end{matrix}\right.\)
ta có x+2>x-1
=>x-1<0 và x+2 >0 để thỏa điều kiện =>x<1 và x>-2(hay -2<x<1)(1)
vì -2<x<1 nên x+7>0
=>x\(\ge\)0 để thỏa điều kiện(2)
từ (1) và (2) =>0\(\le\)x<1
b)
\(\left\{{}\begin{matrix}\left(x-3\right)\left(\sqrt{2}-x\right)>0\\4x-3< 2\left(x+3\right)\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}\left(x-3\right)\left(\sqrt{2}-x\right)>0\\2x-9< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}\left(x-3\right)\left(\sqrt{2}-x\right)>0\\x< \dfrac{9}{2}\end{matrix}\right.\)
có 2 TH xảy ra để thỏa điều kiện
TH1 (x-3)<0 và (\(\sqrt{2}\)-x)<0=>\(\sqrt{2}\)<x<3(nhận)
TH2 (x-3)>0 và (\(\sqrt{2}\)-x)>0=>3<x<\(\sqrt{2}\)(loại)
em nghĩ như nào làm như v thôi có gì sai chị xem và sửa hộ em nhá ![]()
Đúng 0
Bình luận (0)
Giúp mình với mn ơi 😓😓😓
Giúp mình với mn ơi 😓😓😓
3.
Pt hoành độ giao điểm:
\(-x=x^3\Rightarrow x\left(x^2+1\right)=0\Rightarrow x=0\)
Pt có 1 nghiệm nên 2 đồ thị cắt nhau tại 1 điểm
4.
\(2^{2x^2-7x+5}=2^5\Rightarrow2x^2-7x+5=5\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{7}{2}\end{matrix}\right.\) \(\Rightarrow x_1+4x_2=14\)
5.
\(B=10a.a^2\sqrt{5}=10\sqrt{5}a^3\)
6.
\(B=\dfrac{1}{3}\pi R^2h\)
7.
Hàm bậc nhất trên bậc nhất nên đơn điệu trên đoạn đã cho
\(\Rightarrow\) min, max rơi vào 2 đầu mút
\(\Rightarrow M.m=y\left(-5\right).y\left(-2\right)=\dfrac{4}{55}\)
8.
\(lnx=-1\Rightarrow x=e^{-1}\)
Pt có 1 nghiệm
9.
Hàm \(y=\left(\dfrac{1}{2}\right)^x\) nghịch biến trên R
10.
\(\log x\ge1\Rightarrow x\ge10\)
D đúng
Đúng 0
Bình luận (0)
Giúp mình với mn ơi 😓😓😓
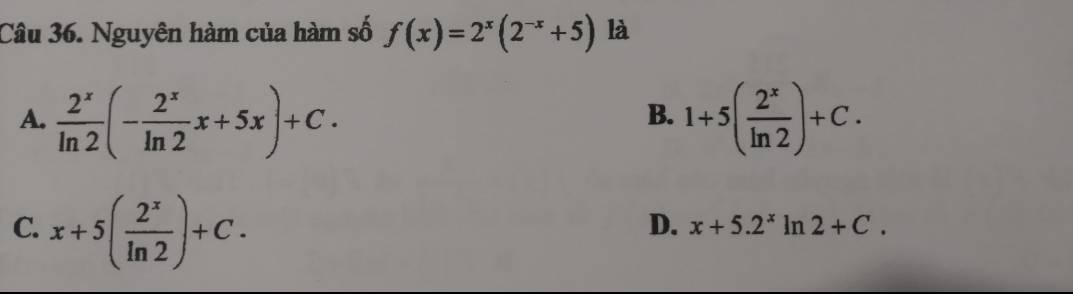
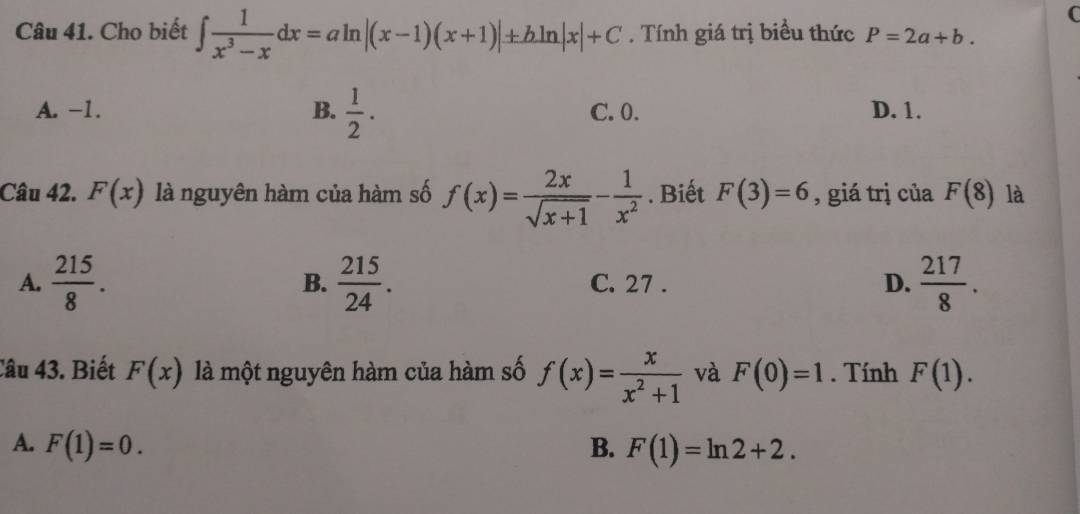

Giúp mình với mn ơi 😓😓😓