Cho hình thang ABCD,AB=9cm,CD=30cm,AD=18cm và BC=20cm.Tính diện tích hình thang ABCD
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TM
Những câu hỏi liên quan
Cho hình thang ABCD(AB//CD). Tính diện tích hình thang ABCD, nếu biết:
a) AB = 4cm, CD = 9cm, BD = 5cm, AC = 12cm.
b) AB= 9cm, CD = 30cm, AD=13cm, BC = 20cm.
Ta áp dụng công thức Brahmagupta để tính
\(s=\frac{\sqrt{\left(AB^2+CD^2+BD^2+AC^2\right)+8\cdot AB\cdot CD\cdot BD\cdot AC-2\left(AB^4+CD^4+BD^4+AC^4\right)}}{4}\)
A) Thay số vào ta đc \(S=6\sqrt{55}\approx44,4972\left(cm^2\right)\)
b) \(S\approx244,1639\left(cm^2\right)\)
hok tốt ...
Đúng 0
Bình luận (0)
Công thức Brahmagupta là công thức tính diện tích của một tứ giác nội tiếp (tứ giác mà có thể vẽ một đường tròn đi qua bốn đỉnh của nó) mà hình thang ko có đường tròn nào đi qua đủ bốn đỉnh của nó nên công thức này ko được áp dụng vào bài này
Đúng 0
Bình luận (0)
Cho hình thang ABCD ( AB//CD ) có AB= 9cm; CD= 30cm; AD=13cm; BC=20cm. Tính S hình thang ABCD ?
1. Cho hình thang ABCD ( AB//CD ) có AB= 9cm; CD= 30cm; AD=13cm; BC=20cm. Tính S hình thang ABCD ?
Cho hình thang abcd vuông tại a và d cho biết ab=12cm cd=18cm,ad=8cm.Tính diện tích hình thang abcd, tỉ số phần trăm diện tích tam giác bcd và diện tích hình thang abcd
ABCD là hình thang vuông tại A và D
=>\(S_{ABCD}=\dfrac{1}{2}\cdot AD\cdot\left(BA+CD\right)=\dfrac{1}{2}\cdot8\cdot\left(12+18\right)=4\cdot30=120\left(cm^2\right)\)
Diện tích tam giác ABD là:
\(S_{ABD}=\dfrac{1}{2}\cdot AB\cdot AD=\dfrac{1}{2}\cdot12\cdot8=4\cdot12=48\left(cm^2\right)\)
Ta có: \(S_{ABD}+S_{BDC}=S_{ABCD}\)
=>\(S_{BDC}+48=120\)
=>\(S_{BDC}=72\left(cm^2\right)\)
=>\(\dfrac{S_{BCD}}{S_{ABCD}}=\dfrac{72}{120}=\dfrac{3}{5}=60\%\)
Đúng 1
Bình luận (0)
B1.Cho hình thang abcd vuông tại a và d cho biết ab=12cm cd=18cm,ad=8cm.Tính diện tích hình thang abcd, tỉ số phần trăm diện tích tam giác bcd và diện tích hình thang abcd
B2.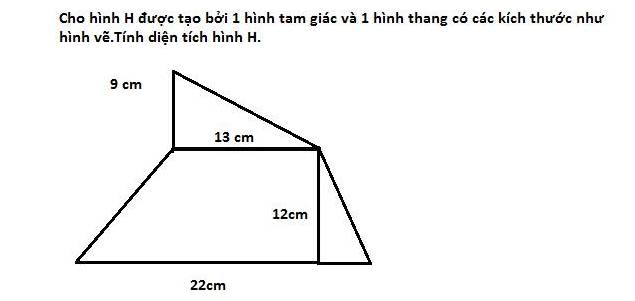
Làm đc tớ xin tặng coin ạ(GẤP);vvv
Bài 1:
Diện tích ABCD: $\frac{(AB+CD)\times AD}{2}=\frac{(12+18)\times 8}{2}=120$ (cm2)
Diện tích $BCD$ là: $CD\times AD:2=8\times 18:2=72$ (cm2)
Tỉ số phần trăm diện tích tam giác BCD và hình thang ABCD là:
$72:120\times 100=60$ (%)
Đúng 0
Bình luận (0)
Bài 2:
Diện tích hình tam giác: $9\times 12:2=58,5$ (cm2)
Diện tích hình thang: $(13+22)\times 12:2=210$ (cm2)
Diện tích hình H là: $58,5+210=268,5$ (cm2)
Đúng 0
Bình luận (0)
Cho hình thang ABCD, đáy nhỏ AB=40cm, đáy lớn CD=60cm, đường cao AD=40cm
a, Tính diện tích hình thang ABCD
b, Lấy E trên AD, G trên BC sao cho ABGE là hình thang và AE=30cm. Tìm cạnh EG
vẽ hình thang ABCD có đáy BC = 9cm, đáy AD = 30cm, cạnh bên AB = 20cm và CD = 13cm
Cho hình thang vuông ABCD, đáy nhỏ AB=30cm, đáy lớn CD=50cm, đường cao AD=40cm. Lấy H trên AD, G trên BC sao cho HG chia hình thang ABCD thành 2 hình thang có đường cao AH=30cm, HD=10cm. Tính diện tích hình thang ABGH và HGCD.
cho hình thang ABCD có đáy ab là 18cm, đáy cd là 27cm,điểm m trên cạnh ad và khoảng cách md=1/3 ad. từ m kẻ đường song song vs đáy cd cắt cạnh bên bc tại n.hãy tính đoạn mn,biết diện tích hình thang abcd là 405cm2

