Cho tam giác ABC, các trung tuyến BM và CN cắt nhau tại G. Gọi P là điểm đối xứng của M qua G; gọi Q là điểm đối xứng của N qua G.
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Nếu tam giác ABC cân tại A thì tứ giác MNPQ hình gì? vì sao? help me
NL
Những câu hỏi liên quan
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?
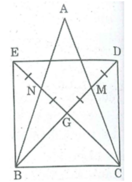
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G
Suy ra: G là trọng tâm của ∆ ABC .
⇒ GB = 2GM (tính chất đường trung tuyến)
GC = 2GN (tính chất đường trung tuyến)
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (l)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (2)
Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét ∆ BCM và ∆ CBN, có: BC cạnh chung
∠ (BCM) = ∠ (CBN) (tính chất tam giác cân)
CM = BN (vì AB = AC)
Suy ra: ∆ BCM = ∆ CBN (c.g.c)
⇒ ∠ (MBC) = ∠ (NCB) ⇒ ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE
Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì ? Vì sao ?
Cho tam giác ABC, các trung tuyến BM và CN cắt nhau ở G. Gọi P là điểm dối xứng của điểm M qua G. Gọi Q là điểm đối xứng của điểm N qua G.Tứ giác MNPQ là hình gì? Vì sao ?
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi
D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là
hình gì? Vì sao?
Cho tam giác ABC các trung tuyến BM;CN cắt nhau tại G gọi P là điểm đối xứng của M qua G ;gọi Q là điểm đối xứng của N qua G
tứ giác MNPQ la hình gì ?
NẾU tam giác ABC cân ở A thì tứ giác MNPQ là hình gì ?vì sao
Cho tam giác ABC, trung tuyến BM, CN cắt nhau tại G. Gọi P là điểm đối xứng của M qua G. Gọi Q là điểm đối xứng của N qua G. a) Tứ giác MNPQ là hình gì? Vì sao? b) Nếu tam giác BAC cân tại A thì tứ giác MNPQ là hình gì? Vì sao?
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điiểm đối xứng G qua M, E đối xứng G qua N. Tứ giác BEDC là hình gì? Vì sao?
Tự vẽ hình:
cminh:Vì D đối xứng với G qua M
=>GM=MD Hay GD=2GM
Vì BM;CN cắt nhau tại G trong tam giác ABC
=>G là trọng tâm trong Tam giác ABC =>BG=2GM
Suy ra : GD=BG(vì =2GM)=> G là trung điểm của BD (1)
Ta lại có : E đối xứng với G qua N=> EN=GN Hay EG=2NG
Và CG=2GN( G là trọng tâm)
Suy ra: CG=EG ( vì =2NG) (2) (*)
Từ (1) (2)=> Tứ giác BEDC là hình bình hành
Xét \(\Delta\)CBM Và \(\Delta\)BCN Có:
BC: Cạnh chung
Góc B=C(g/t)
BN=CM(AB=AC)
=> hai tam giác bằng nhau(c-g-c)
=>MBC=NCB(2 góc tương ứng) hay tam giác GBC cân=> BG=GC (**)
Từ (*) (**)=> Hình bình hành BEDC là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC các trung tuyến BM , CN cắt tại G . Gọi P là điểm đối xứng với M qua O gọi Q là điểm đối xứng N qua G .
a : Tính tứ giác MNPQ
b : Nếu tam giác ABC cân thì MNPQ là hcn
Cho tam giác ABC các trung tuyến BM , CN cắt tại G . Gọi P là điểm đối xứng với M qua O gọi Q là điểm đối xứng N qua G .
a : Tính tứ giác MNPQ
b : Nếu tam giác ABC cân thì MNPQ là hcn