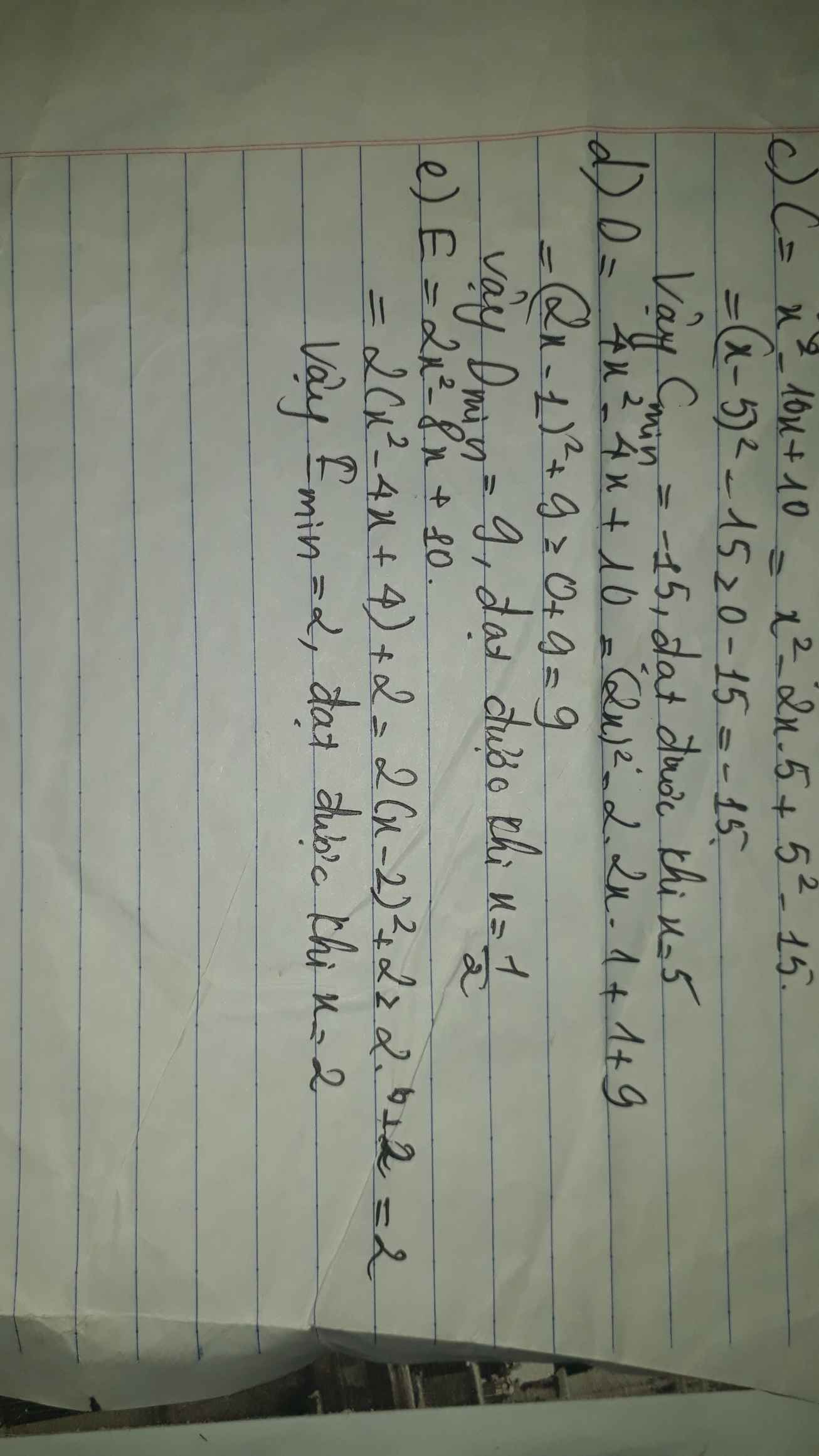Tìm GTNN của A = x 2 +8x+10
VO
Những câu hỏi liên quan
Tìm GTNN của
a) A= \(x^2+4x+10\)
b) B= \(x^2-2x+10\)
c) C= \(x^2-10x+10\)
d) D= \(4x^2-4x+10\)
e) E= \(2x^2-8x+10\)
Giup mk vs ai làm nhanh mk sẽ vote cho bạn đó
a) Ta có: \(A=x^2+4x+10\)
\(=x^2+4x+4+6\)
\(=\left(x+2\right)^2+6\ge6\forall x\)
Dấu '=' xảy ra khi x=-2
b) Ta có: \(B=x^2-2x+10\)
\(=x^2-2x+1+9\)
\(=\left(x-1\right)^2+9\ge9\forall x\)
Dấu '=' xảy ra khi x=2
c) Ta có: \(C=x^2-10x+10\)
\(=x^2-10x+25-15\)
\(=\left(x-5\right)^2-15\ge-15\forall x\)
Dấu '=' xảy ra khi x=5
d) Ta có: \(D=4x^2-4x+10\)
\(=4x^2-4x+1+9\)
\(=\left(2x-1\right)^2+9\ge9\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
Tìm GTLN - GTNN của các biểu thức ?* bài 1: Tìm GTNN: a) A (x - 5)² + (x² - 10x)² - 24 b) B (x - 7)² + (x + 5)² - 3 c) C 5x² - 6x +1 d) D 16x^4 + 8x² - 9 e) A (x + 1)(x - 2)(x - 3)(x - 6) f) B (x - 2)(x - 4)(x² - 6x + 6) g) C x^4 - 8x³ + 24x² - 8x + 25 h) D x^4 + 2x³ + 2x² + 2x - 2 i) A x² + 4xy + 4y² - 6x – 12y +4 k) B 10x² + 6xy + 9y² - 12x +15 l) C 5x² - 4xy + 2y² - 8x – 16y +83 m) A (x - 5)^4 + (x - 7)^4 – 10(x - 5)²(x - 7)² + 9 * Bài 2: Tìm GTLN: a) M -7x² + 4x -12 b) N -16x² - 3x +14 c) M...
Đọc tiếp
Tìm GTLN - GTNN của các biểu thức ?
* bài 1: Tìm GTNN:
a) A= (x - 5)² + (x² - 10x)² - 24
b) B= (x - 7)² + (x + 5)² - 3
c) C= 5x² - 6x +1
d) D= 16x^4 + 8x² - 9
e) A= (x + 1)(x - 2)(x - 3)(x - 6)
f) B= (x - 2)(x - 4)(x² - 6x + 6)
g) C= x^4 - 8x³ + 24x² - 8x + 25
h) D= x^4 + 2x³ + 2x² + 2x - 2
i) A= x² + 4xy + 4y² - 6x – 12y +4
k) B= 10x² + 6xy + 9y² - 12x +15
l) C= 5x² - 4xy + 2y² - 8x – 16y +83
m) A= (x - 5)^4 + (x - 7)^4 – 10(x - 5)²(x - 7)² + 9
* Bài 2: Tìm GTLN:
a) M= -7x² + 4x -12
b) N= -16x² - 3x +14
c) M= -x^4 + 4x³ - 7x² + 12x -5
d) N= -(x² + x – 2) (x² +9x+18) +27
* Bài 3:
1) Cho x - 3y = 1. Tìm GTNN của M= x² + 4y²
2) Cho 4x - y = 5. Tìm GTNN của 3x²+2y²
3) Cho a + 2b = 2. Tìm GTNN của a³ + 8b³
* Bài 4: Tìm GTLN và GTNN của các biểu thức:
1) A = (3 - 4x)/(x² + 1)
2) B= (8x + 3)/(4x² + 1)
3) C= (2x+1)/(x²+2)
Tìm GTNN của
A=2.x^2+8x-24
Tìm GTLN của
B=-x^2-8x+5
\(A=2x^2+8x-24\)
\(=2\left(x^2+4x-12\right)\)
\(=2\left[x^2+4x-4-8\right]\)
\(=2\left[\left(x-2\right)^2-8\right]\)
\(\left(x-2\right)^2\ge0\)
\(\Rightarrow\left(x-2\right)^2-8\ge-8\)
\(\Rightarrow2\left[\left(x-2\right)^2-8\right]\ge-16\)
Do đó GTNN của A là -16 khi \(x-2=0\Rightarrow x=2\)
Đúng 0
Bình luận (0)
\(B=x^2-8x+5=x^2-8x+16-9\)
\(=x^2-2\left(4x\right)+4^2-9\)
\(=\left(x-4\right)^2-9\)
\(\left(x-4\right)^2\ge0\)
\(\Rightarrow\left(x-4\right)^2-9\ge-9\)
Do đó GTNN của B là -9 khi \(x-4=0\Rightarrow x=4\)
Đúng 0
Bình luận (0)
Tìm gtnn, gtln của A= x^2+8x+15 B= 7x-x^2-5
1) \(A=x^2+8x+15=\left(x^2+8x+16\right)-1=\left(x+4\right)^2-1\ge-1\)
\(minA=-1\Leftrightarrow x=-4\)
2) \(B=7x-x^2-5=-\left(x^2-7x+\dfrac{49}{4}\right)+\dfrac{29}{4}=-\left(x-\dfrac{7}{2}\right)^2+\dfrac{29}{4}\le\dfrac{29}{4}\)
\(maxB=\dfrac{29}{4}\Leftrightarrow x=\dfrac{7}{2}\)
Đúng 1
Bình luận (1)
Ta có: \(A=x^2+8x+15\)
\(=x^2+8x+16-1\)
\(=\left(x+4\right)^2-1\ge-1\forall x\)
Dấu '=' xảy ra khi x=-4
Đúng 0
Bình luận (0)
Tìm GTNN của A
\(A=\frac{x^4+2x^3+8x+16}{x^4-2x^3+8x^2-8x+16}\)
Bài 1:
a, Tìm GTNN của A = \(4x^2+4x+11\)
b, Tìm GTLN của B = \(5-8x-x^2\)
I zì:vv
a) Ta có: \(A=4x^2+4x+11=4x^2+4x+1=10=\left(2x+1\right)^2+10\ge10\forall x\)
Vậy MinA=10 khi \(x=-\dfrac{1}{2}\)
b) Ta có: \(B=5-8x-x^2=-\left(x^2+8x-5\right)=-\left(x^2+8x+16-21\right)\)
\(=-\left(x+4\right)^2+21\le21\forall x\)
Vậy MaxB=21 khi x=-4
Đúng 2
Bình luận (9)
Tìm gtln ( hoặc gtnn ):
a) \(A=2x^2-8x-10\)
b) \(B=x-x^2\)
a, \(A=2x^2-8x-10=2\left(x^2-4x+4\right)-18=2\left(x-2\right)^2-18\ge-18\)
Dấu "=" xảy ra <=> x-2=0 <=> x=2
Vậy MinA = -18 khi x=2
b, \(B=x-x^2=-\left(x^2-x+\frac{1}{4}\right)+\frac{1}{4}=-\left(x-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\)
Dấu "=" xảy ra <=> x-1/2=0 <=> x=1/2
Vậy MaxB = 1/4 khi x=1/2
Đúng 0
Bình luận (0)
a) \(A=2x^2-8x-10\)
\(=2\left(x^2-4x-5\right)\)
\(=2\left(x^2-2.x.2+2^2-2^2-5\right)\)
\(=2\left[\left(x-2\right)^2-9\right]\)
\(=2\left(x-2\right)^2-18\)
Vì \(2\left(x-2\right)^2\ge0\forall x\)
Nên \(2\left(x-2\right)^2\ge-18\)
Hay \(A\ge-18\)
Vậy gtnn của A là -18 khi \(2\left(x-2\right)^2=0\)
\(x-2=0\)
\(x=2\)
b) \(B=x-x^2\)
\(=-x^2-x\)
\(=-\left(x^2-x\right)\)
\(=-\text{[}x^2-2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2\text{]}\)
\(=-\text{[}\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\text{]}\)
\(=-\left(x-\frac{1}{2}\right)^2+\frac{1}{4}\)
Vì \(-\left(x-\frac{1}{2}\right)^2\le0\forall x\)
Nên \(-\left(x-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\forall x
\)
Vậy gtln của B là \(\frac{1}{4}\)khi \(x-\frac{1}{2}=0\)
\(x=\frac{1}{2}\)
Đúng 0
Bình luận (0)
tìm GTNN của đa thức sau: -8x^2 +4xy -y^2+10
Bài 1: Tìm GTNN và GTLN của \(A=123+\sqrt{-x^2+6x+5}\)
Bài 2:Tìm GTNN và GTLN của \(A=\sqrt{-x^2+8x-12}-7\)
Bài 3: Tìm GTNN và GTLN của \(A=\sqrt{-x^2-x+4}\)