rút gọn rồi tính: C=\(\sqrt{-9a^2-\sqrt{9+12a+4a^2}}\)
với a=-9
NT
Những câu hỏi liên quan
rút gọn biểu thức:\(\sqrt{4a^2+12a+9}+\sqrt{4a^2-12a+9}\) với\(-\dfrac{3}{2}\le a\le\dfrac{3}{2}\)
giúp tui nha,tui đang gấp lắm
\(\sqrt{4a^2+12a+9}+\sqrt{4a^2-12a+9}\) với \(-\dfrac{3}{2}\le a\le\dfrac{3}{2}\)
\(\sqrt{\left(2a+3\right)^3}+\sqrt{\left(2a-3\right)^3}\)
\(\left|2a+3\right|+\left|2a-3\right|\)
\(2a+3-2a+3\)
\(6\)
Đúng 1
Bình luận (0)
Cho \(A=\sqrt{9a^4-6a^2+1}-\sqrt{4a^4+12a^2+9}\)
a. Rút gọn A
b. Tính A khi a=\(\sqrt{5}\)
\(\sqrt{-9a}-\sqrt{9+12a+4a^2}\) TAI a= -9
rut gọn roi tinh
\(\sqrt{-9a}-\sqrt{4a^2+12a+9}=3\sqrt{-a}-\left|2a+3\right|\)
Thay a = -9 vào được kết quả là : -6
Đúng 0
Bình luận (0)
Rút gọn:\(\frac{\sqrt{9+12a+4a^2}}{\sqrt{b^2}}\)với 0>a>=\(\frac{-3}{2}\), b<0
\(\frac{\sqrt{9+12a+4a^2}}{\sqrt{b^2}}\)
\(=\frac{\sqrt{\left(2a+3\right)^2}}{\sqrt{b^2}}\)
\(=\frac{2a+3}{-b}\)( theo điều kiện )
Đúng 0
Bình luận (0)
bố mày đéo biết
\(\frac{\sqrt{9+12a+4a^2}}{\sqrt{b^2}}\)
\(=\frac{\sqrt{3^2+2.3.2a+\left(2a\right)^2}}{\sqrt{b^2}}\)
\(=\frac{\sqrt{\left(3+2a\right)^2}}{\sqrt{b^2}}\)
\(=\frac{|3+2a|}{|b|}\)
Vì \(b< 0\Rightarrow|b|=-b\)
Vì \(a\ge-1.5\) nên \(3+2a\ge0\)
Vậy : | 3 + 2a | = 3 + 2a
Rút gọn rồi tính giá trị các biểu thức sau: - 9 a - 9 + 12 a + 4 a 2 t ạ i a = - 9
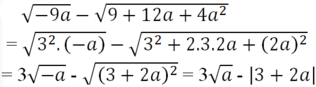
Tại a = -9 ta được:
= 3√-(-9) - |3 + 2(-9)|
= 3√32 - |3 - 18|
= 3.3 - |-15| = 9 - 15 = -6
Đúng 0
Bình luận (0)
Rút gọn rồi tính giá trị các biểu thức sau:
a
)
−
9
a
−
9
+
12
a
+
4
a
2
t
a
i
...
Đọc tiếp
Rút gọn rồi tính giá trị các biểu thức sau:
a ) − 9 a − 9 + 12 a + 4 a 2 t a i a = − 9 b ) 1 + 3 m m − 2 m 2 − 4 m + 4 tai m = 1 , 5 c ) 1 − 10 a − 25 a 2 − 4 a t a i a = 2 d ) 4 x − 9 x 2 + 6 x + 1 t a i x = − 3
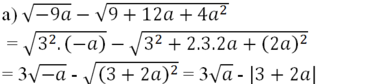
Tại a = -9 ta được:
= 3√-(-9) - |3 + 2(-9)|
= 3√32 - |3 - 18|
= 3.3 - |-15| = 9 - 15 = -6
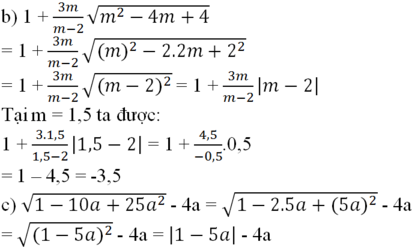
Tại a = √2 ta được:
= |1 - 5√2| - 4√2
= (5√2 - 1) - 4√2
= √2 - 1
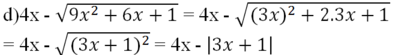
Tại x = -√3 ta được:
= 4(-√3) - |3(-√3) + 1|
= -4√3 - |-3√3 + 1|
= -4√3 - (3√3 - 1)
= -7√3 + 1
Đúng 0
Bình luận (0)
TN
8 tháng 11 2021 lúc 12:48
Rút gọn các biểu thức sau
a) \(\sqrt{25a^2}+3a\) với a ≥ 0
b) \(\sqrt{9a^4}+3a^2\)
c) \(5\sqrt{4a^6}-3a^3\) với a < 0
a) \(=5\left|a\right|+3a=5a+3a=8a\)
b) \(=3\left|a^2\right|+3a^2=3a^2+3a^2=6a^2\)
c) \(=5.2\left|a^3\right|-3a^3=-10a^3-3a^3=-13a^3\)
Đúng 1
Bình luận (6)
Rút gọn:a/
\(\sqrt{-9a}-\sqrt{9+12a+4a^2}\)
b/\(1+\frac{3m}{m-2}\sqrt{m^2-4m+4}\)
c/\(4x-\sqrt{9x^2+6x+1}\)
\(a)\sqrt{-9a}-\sqrt{9+12a+4a^2}\)
\(==\sqrt{3^2.\left(-a\right)}-\sqrt{3^2-2.3.2a+\left(2a\right)^2}\)
\(=3\sqrt{-a}-\sqrt{\left(3+2a\right)^2}\)
\(=3\sqrt{a}-\left|3+2a\right|\)
\(b)1+\frac{3m}{m-2}\sqrt{m^2-4m+4}\)
\(=1+\frac{3m}{m-2}\sqrt{\left(m\right)^2-2.2m+2^2}\)
\(=1+\frac{3m}{m-2}\sqrt{\left(m-2\right)^2}\)
\(=1+\frac{3m}{m-2}|m-2|\)
\(c)4x-\sqrt{9x^2+6x+1}\)
\(=4x-\sqrt{\left(3x\right)^2+2.3x+1}\)
\(=4x-\sqrt{\left(3x+1\right)^2}\)
\(=4x-|3x+1|\)
Rút gọn các biểu thức sau:
a) $\sqrt{9a^4}$
b) 2$\sqrt{a^{2}}$- 5a (với a<0)
c) $\sqrt{16(1+4x+4x^2)}$ với x $\geq$ $\frac{1}{2}$
d) $\frac{1}{a-3}$$\sqrt{9(a^2-3a+9)}$ với a<3
a) \(\sqrt{9a^4}=\sqrt{\left(3a^2\right)^2}=\left|3a^2\right|=3a^2\)
b) \(2\sqrt{a^2}-5a=2\left|a\right|-5a=-2a-5a=-7a\)
c) \(\sqrt{16\left(1+4x+4x^2\right)}=\sqrt{\left[4\left(1+2x\right)\right]^2}=\left|4\left(1+2x\right)\right|=4\left(1+2x\right)\)
Đúng 3
Bình luận (0)