THAY TẤT CẢ =0 THÀNH >0 HOẶC < 0 NHÉ 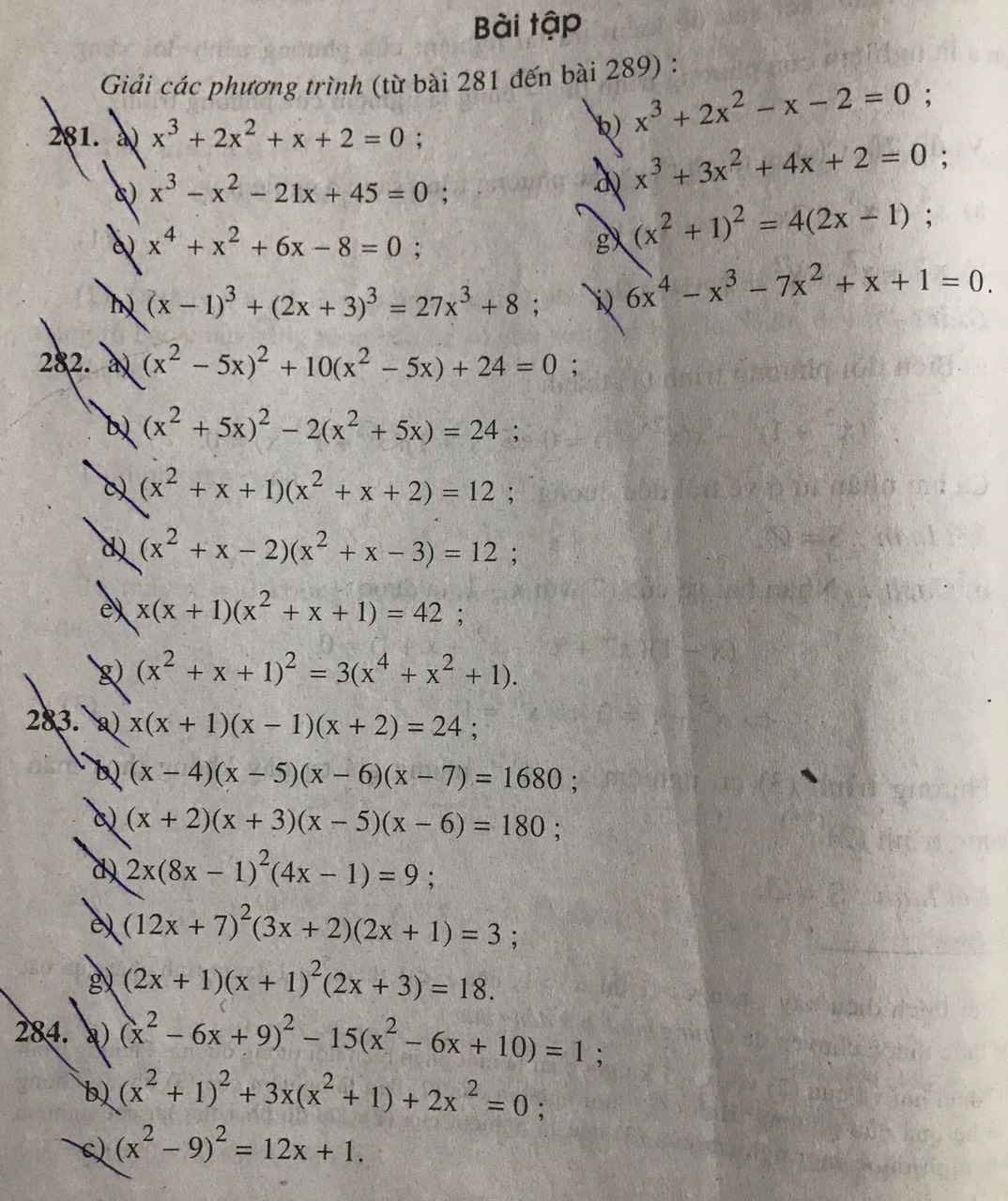
HM
Những câu hỏi liên quan
Cho một bảng biến đổi ô vuông 4*4. Trên các ô, ban đầu ghi 9 số 1 và 7 số 0 một cách tùy ý ( mỗi ô ghi 1 số ). Với mỗi phép biến đổi bảng, cho phép chọn một hàng hoặc một cột bất kỳ thực hiện phép biến đổi tất cả số 1 thành số 0 và ngược lại, số 0 thành số 1 trên các cột hoặc hàng đã chọn. Vậy, có thể đưa toàn bộ bảng về số 0 sau một phép biến đổi không? tại sao?Nhanh lên nhé, tớ đang vội, ai trả lời nhanh nhất mình tick cho nhé!!!
Đọc tiếp
Cho một bảng biến đổi ô vuông 4*4. Trên các ô, ban đầu ghi 9 số 1 và 7 số 0 một cách tùy ý ( mỗi ô ghi 1 số ). Với mỗi phép biến đổi bảng, cho phép chọn một hàng hoặc một cột bất kỳ thực hiện phép biến đổi tất cả số 1 thành số 0 và ngược lại, số 0 thành số 1 trên các cột hoặc hàng đã chọn. Vậy, có thể đưa toàn bộ bảng về số 0 sau một phép biến đổi không? tại sao?
Nhanh lên nhé, tớ đang vội, ai trả lời nhanh nhất mình tick cho nhé!!!
Câu trả lời là không. Và lời giải khá đơn giản. Thay dấu cộng bằng số 1 và dấu trừ bằng - 1. Xét tích tất cả các số trên bảng vuông. Khi đó, qua mỗi phép biến đổi, tích này không thay đổi (vì sẽ đổi dấu 4 số). Vì vậy, cho dù ta thực hiện bao nhiêu lần, từ bảng vuông (1, 15) sẽ chỉ đưa về các bảng vuông có số lẻ dấu -, có nghĩa là không thể đưa về bảng có toàn dấu cộng.
Bạn tham khảo nha
Đúng 0
Bình luận (0)
Cho một bảng biến đổi ô vuông 4*4. Trên các ô, ban đầu ghi 9 số 1 và 7 số 0 một cách tùy ý ( mỗi ô ghi 1 số ). Với mỗi phép biến đổi bảng, cho phép chọn một hàng hoặc một cột bất kỳ thực hiện phép biến đổi tất cả số 1 thành số 0 và ngược lại, số 0 thành số 1 trên các cột hoặc hàng đã chọn. Vậy, có thể đưa toàn bộ bảng về số 0 sau một số phép biến đổi không? tại sao?Nhanh lên nhé, tớ đang vội, ai trả lời nhanh nhất mình tick cho nhé!!! Câu hỏi tương tự Đọc thêm Báo cáoToán lớp 9
Đọc tiếp
Cho một bảng biến đổi ô vuông 4*4. Trên các ô, ban đầu ghi 9 số 1 và 7 số 0 một cách tùy ý ( mỗi ô ghi 1 số ). Với mỗi phép biến đổi bảng, cho phép chọn một hàng hoặc một cột bất kỳ thực hiện phép biến đổi tất cả số 1 thành số 0 và ngược lại, số 0 thành số 1 trên các cột hoặc hàng đã chọn. Vậy, có thể đưa toàn bộ bảng về số 0 sau một số phép biến đổi không? tại sao?
Nhanh lên nhé, tớ đang vội, ai trả lời nhanh nhất mình tick cho nhé!!!
Câu hỏi tương tự Đọc thêm Báo cáo
Toán lớp 9
Chúc mừng các thầy cô nhân ngày 20/11. Kính chúc các thầy cô luôn mạnh khỏe, hạnh phúc, thành đạt trong sự nghiệp trồng người nhé !
p/s; Lời chúc này gửi đến tất cả mn làm nghề nhà giáo nak ^-^
Em chúc thầy cô trên olm mạnh khỏe , và đừng bất cẩn trong việc trừ điểm nha ^^
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chỉ mình ạ! a^2b ; a^2 b .* Xét từng trường hợp b0 , b0 , b0.* Còn a thì sao ạ có các trường hợp như trên không giải thích! * Nếu mà đang lớn hơn, nhỏ hơn thêm dấu bằng vào thành lớn hơn hoặc bằng, nhỏ hơn hoặc bằng thì nó có bị thay đổi gì không. Nếu có thì giải thihs giúp mình ạ! --------------------------------------------------a^2ge b^2 và a^2le b^2 có giống tương tự như bài trên hay không giải tích giúp mình ạ! Nếu khác các bạn lại viết rõ ra nhé! * Ngoài ra các anh chị học nhiều hiểu rộng...
Đọc tiếp
Chỉ mình ạ! \(a^2>b\) ; \(a^2< b\) .
* Xét từng trường hợp b<0 , b=0 , b>0.
* Còn a thì sao ạ có các trường hợp như trên không giải thích!
* Nếu mà đang lớn hơn, nhỏ hơn thêm dấu bằng vào thành lớn hơn hoặc bằng, nhỏ hơn hoặc bằng thì nó có bị thay đổi gì không. Nếu có thì giải thihs giúp mình ạ!
--------------------------------------------------
\(a^2\ge b^2\) và \(a^2\le b^2\) có giống tương tự như bài trên hay không giải tích giúp mình ạ! Nếu khác các bạn lại viết rõ ra nhé!
* Ngoài ra các anh chị học nhiều hiểu rộng hơn rồi còn những công thức nào như trên liệt kê ra giúp mình trong các trường hợp giải bài tập nhé ạ! Em cảm ơn ạ!
* Giups mình chi tiết nhá!
Em không nêu ra yêu cầu và các điều kiện liên quan của đề bài thì làm sao mn giúp em được?
Đúng 0
Bình luận (2)
camcon :
Ví dụ như của em: Giải bất phương trình $x^2>4$.
Ta đưa về dạng 1 vế chứa 0 như sau:
$x^2>4$
$\Leftrightarrow x^2-4>0$
$\Leftrightarrow (x-2)(x+2)>0$
Đến đây ta có 2 TH xảy ra:
TH1: \(\left\{\begin{matrix} x-2>0\\ x+2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>2\\ x>-2\end{matrix}\right.\Rightarrow x>2\)
TH2: \(\left\{\begin{matrix} x-2< 0\\ x+2< 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x< 2\\ x< -2\end{matrix}\right.\Rightarrow x< -2\)
Vậy tóm lại $x>2$ hoặc $x< -2$
Đúng 1
Bình luận (6)
Tìm tất cả các số nguyên x biết:-1/2<x/3< hoặc =0
\(\frac{-1}{2}<\frac{x}{3}\le0\) đây là đề
Đúng 0
Bình luận (0)
1:tìm tất cả các giá trị của x thỏa mãn |x+1|-2|x-1|-x=0
2:tìm tất cả các giá trị của x, y thỏa mãn | x-2|-|4x-8|-y^2=0
giúp mình nhé!mình cần gấp
Tìm tất cả các giá trị thực của tham số m để phưong trình x^2-4x+3-m=0 có 2 nghiệm phân biệt x1,x2 sao cho 0 nhỏ hơn hoặc bằng x1
Để phương trình 1 có 2 nghiệm phân biệt thì : \(\Delta>0\)
\(\Leftrightarrow\left(-4\right)^2-4\left(3-m\right)>0\\ \Leftrightarrow4+4m>0\\ \Leftrightarrow m>-1\circledast\)
Vì phương trình 1 cso hai nghiệm phân biệt
=> \(x_1=\dfrac{4-\sqrt{4+4m}}{2}\)
Theo bài ra ta có phương trình 1 cso 2 no phân biệt với \(x_1\le0\)
\(\Leftrightarrow\dfrac{4-\sqrt{4+4m}}{2}\le0\)
Mà ta có 2 > 0
\(\Rightarrow4-\sqrt{4+4m}\le0\\ \Leftrightarrow m\ge3\circledast\circledast\)
Từ * và ** thì với giá trị \(m\ge3\) thì bài toán được t/m
Đúng 0
Bình luận (0)
Tìm tất cả tham số `m` để bất phương trình `x^2-x+m(1-m)<=0` là hệ quả của bất phương trình `\sqrt{\sqrt{x-1}+4}-\sqrt{\sqrt{x-1}+1}>=1`?
`A.m=1/2`
`B.m<=0` hoặc `m>=1`
`C.m>=1`
`D.m<=0`
Với m = 1/2 thì bpt (1) \(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2\le0\Leftrightarrow x=\dfrac{1}{2}\)
bpt(2) \(\sqrt{\sqrt{x-1}+4}-\sqrt{\sqrt{x-1}+1}\ge1\) ( ĐK : \(x\ge1\) )
\(\Leftrightarrow\sqrt{\sqrt{x-1}+4}\ge1+\sqrt{\sqrt{x-1}+1}\)
\(\Leftrightarrow\sqrt{x-1}+4\ge1+\sqrt{x-1}+1+2\sqrt{\sqrt{x-1}+1}\)
\(\Leftrightarrow2\ge2\sqrt{\sqrt{x-1}+1}\Leftrightarrow1\ge\sqrt{\sqrt{x-1}+1}\) \(\Leftrightarrow\sqrt{x-1}+1\le1\Leftrightarrow\sqrt{x-1}\le0\Leftrightarrow x=1\)
bpt (2) có no x = 1 . Loại A
Với m khác 1/2 \(x^2-x+m\left(1-m\right)\le0\)
\(\Leftrightarrow x^2-m^2-\left(x-m\right)\le0\) \(\Leftrightarrow\left(x-m\right)\left(x+m-1\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge m;x\le1-m\\x\le m;x\ge1-m\end{matrix}\right.\)
Vì bpt (1) là hệ quả bpt (2) nên bpt (1) có no x = 1
Khi đó : \(\left[{}\begin{matrix}1\ge m;1\le1-m\\1\le m;1\ge1-m\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\le0\\m\ge1\end{matrix}\right.\)
Chọn B
Đúng 2
Bình luận (0)
Tìm tất cả tham số mm để bất phương trình x2−x+m(1−m)≤0x2-x+m(1-m)≤0 là hệ quả của bất phương trình √√x−1+4−√√x−1+1≥1x-1+4-x-1+1≥1?
A.m=12A.m=12
B.m≤0B.m≤0 hoặc m≥1m≥1
C.m≥1C.m≥1
D.m≤0D.m≤0
Đúng 1
Bình luận (0)
Cho P(x) là đa thức có tất cả các hệ số là số tự nhiên bé hơn hoặc bằng 17 và có P(17)=2010. Tính P(x).
Bài giải:
Nhìn qua người ta tưởng lầm bài toán này khó lòng giải quyết được. Nhưng nếu hiểu rõ thì hs lớp 7 dư sức làm quá đi chứ. ĐS: P(x) = 6x^2 + 16x + 4. Tuy nhiên trình bày bài giải cũng hơi mệt nên nói cách làm thôi ạ.
(Các số n, n-1, n-2,.. vui lòng hiểu là để trong ngoặc đơn kẻo lộn)
Gọi P(x) = a_n . x^n + a_n-1 . x^n-1 + a_n-2 . x^n-2 + a_1.x + a_0
với a_n, a_n-1, a_n-2,... a_1, a_0 là các hệ số tự nhiên bé hơn 17. (1)
P(17) = 17^n. a_n + 17^n-1. a_n-1 + ... + 17.a_1 + a_0
:::::::::= 17. (17^n-1. a_n + 17^n-2. a_n-1 + ... + 17.a_2 + a_1) + a_0
:::::::::= 17. P_1(17) + a_0 = 2010 (gọi biểu thức trong ngoặc đơn là P_1(x) )
(1) => a_0 < 17 => a_0 = 4 (số dư khi chia 2010 cho 17)
P_1(17) = 118 (phần nguyên khi chia 2010 cho 17)
Tương tự với P_1(17):
P_1(17) = 17.(17^n-2. a_n + 17^n-3 + ... + a_2) + a_1
::::::::::::= 17. P_2(17) + a_1 = 118 (gọi bt trong ngoặc đơn là P_2(x) )
(1) => a_0 < 17 => a_1 = 16 (số dư khi chia 118 cho 17)
P_2(17) = 6 < 17. (phù, quá trình kết thúc vì P_2(x) là 1 đa thức bậc 0 chỉ có hệ số tự do)
=> a_2 = P_2(17) = 6
Đa thức P(x) có bậc 2 và có dạng P(x) = 6x^2 + 16x + 4.
Làm xong mỏi hết cả tay!!!
Đúng 0
Bình luận (0)




