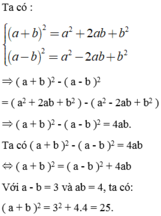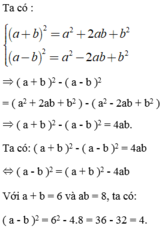chứng minh : (a-b)2=(a+b)2+4ab
HN
Những câu hỏi liên quan
chứng minh:
(a+b)2=(a-b)2+4ab
(a-b)2=(a-b)-4ab
\(\left(a+b\right)^2=a^2+2ab+b^2\)(1)
\(\left(a-b\right)^2+4ab=a^2-2ab+b^2+4ab=a^2+2ab+b^2\)(2)
từ (1) và (2) => đpcm
\(\left(a-b\right)^2=a^2-2ab+b^2\)(3)
\(\left(a+b\right)^2-4ab=a^2+2ab+b^2-4ab=a^2-2ab+b^2\)(4)
từ (1) và (2) => đpcm
Đúng 0
Bình luận (0)
Chứng minh rằng:
(a + b)2 = (a – b)2 + 4ab
(a – b)2 = (a + b)2 – 4ab
Áp dụng:
a) Tính (a – b)2, biết a + b = 7 và a.b = 12.
b) Tính (a + b)2, biết a – b = 20 và a.b = 3.
+ Chứng minh (a + b)2 = (a – b)2 + 4ab
Ta có:
VP = (a – b)2 + 4ab = a2 – 2ab + b2 + 4ab
= a2 + (4ab – 2ab) + b2
= a2 + 2ab + b2
= (a + b)2 = VT (đpcm)
+ Chứng minh (a – b)2 = (a + b)2 – 4ab
Ta có:
VP = (a + b)2 – 4ab = a2 + 2ab + b2 – 4ab
= a2 + (2ab – 4ab) + b2
= a2 – 2ab + b2
= (a – b)2 = VT (đpcm)
+ Áp dụng, tính:
a) (a – b)2 = (a + b)2 – 4ab = 72 – 4.12 = 49 – 48 = 1
b) (a + b)2 = (a – b)2 + 4ab = 202 + 4.3 = 400 + 12 = 412.
Đúng 0
Bình luận (0)
Chứng minh rằng
a/ (a+b)^2=(a-b)^2+4ab
b/ (a-b)^2=(a+b)^2-4ab
c/ (a^2+b^2)(x^2+y^2)=(ax-by)^2+(ay+bx)^2
a) \(\left(a+b\right)^2=a^2+2ab+b^2\left(1\right)\)
\(\left(a-b\right)^2+4ab=a^2-2ab+b^2+4ab=a^2-2ab+4ab+b^2=a^2+2ab+b^2\left(2\right)\)
Từ (1) và (2) => đpcm
b) \(\left(a-b\right)^2=a^2-2ab+b^2\left(3\right)\)
\(\left(a+b\right)^2-4ab=a^2+2ab+b^2-4ab=a^2+2ab-4ab+b^2=a^2-2ab+b^2\left(4\right)\)
Từ (3) và (4) =>đpcm
c) \(\left(a^2+b^2\right)\left(x^2+y^2\right)=a^2\left(x^2+y^2\right)+b^2\left(x^2+y^2\right)\)
\(=a^2x^2+a^2y^2+b^2x^2+b^2y^2\left(5\right)\)
\(\left(ax-by\right)^2+\left(ay+bx\right)^2=a^2x^2-2axby+b^2y^2+a^2y^2+2aybx+b^2x^2\)
\(=a^2x^2+a^2y^2+b^2x^2+b^2y^2\left(6\right)\)
Từ (5) và (6) =>đpcm
Đúng 0
Bình luận (0)
Chứng minh rằng
a) (a+b)^2 = (a-b)^2 +4ab
b) (a-b)^2 = (a+b)^2 - 4ab
c)( a^2 + b^2 ).(x^2 +y^2) = (ax - by)^2 +(ay+bx)^2
a) VP=(a-b)2+4ab
=a2-2ab+b2+4ab
=a2+b2+2ab
=(a+b)2=VT
Vậy (a+b)^2 = (a-b)^2 +4ab
b) VP=(a+b)2-4ab
=a2+2ab+b2-4ab
=a2-2ab+b2
=(a-b)2=VT
Vậy (a-b)^2 = (a+b)^2 - 4ab
c)
VP=(ax-by)2+(ay+bx)2
=a2x2-2axby+b2y2+a2y2+2axby+b2x2
=a2x2+b2y2+a2y2+b2x2
=(a2x2+b2x2)+(b2y2+a2y2)
=x2.(a2+b2)+y2.(a2+b2)
=(a2+b2)(a2+y2)=VT
Vậy ( a^2 + b^2 ).(x^2 +y^2) = (ax - by)^2 +(ay+bx)^2
Đúng 0
Bình luận (0)
Chứng minh hằng đẳng thức:
1) (a+b)^2-(a-b)^2=4ab
3) (a+b)^2-4ab=(a-b)^2
5) a^3+b^3=(a+b)^3-3ab(a+b)
1) biến đổi vế trái:
= a2+2ab+b2 -a2 +2ab -b2
=4ab = vế phải ( đpcm)
3;5 tuong tu
Đúng 0
Bình luận (0)
1) (a + b)2 - (a - b)2 = a2 + 2ab + b2 - a2 + 2ab - b2 = 4ab
3) (a + b)2 - 4ab = a2 + 2ab + b2 - 4ab = a2 - 2ab + b2 = (a - b)2
5) a3 + b3 = a3 + 3a2b + 3ab2 + b3 - 3a2b - 3ab2 = (a + b)3 - 3ab(a + b)
Đúng 0
Bình luận (0)
1) (a+b)^2 - (a-b)^2 = 4ab
VT= (a + b - a +b) (a+b + a-b)
= 2b * 2a
= 4ab = VP
Vậy (a+b)^2 - (a-b)^2 = 4ab
2) (a+b)^2 - 4ab = (a-b)^2
VT= (a+b)^2 - 4ab
= a^2 + 2ab + b^2 - 4ab
= a^2 - 2ab + b^2
= (a-b)^2 = VP
Vậy (a+b)^2 - 4ab = (a-b)^2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh đẳng thức ( a-b)^2 = ( a+b)^2 - 4ab
Ta có: \(VP=\left(a+b\right)^2-4ab\)
\(=a^2+2ab+b^2-4ab\)
\(=a^2-2ab+b^2\)
\(=\left(a-b\right)^2=VT\)(đpcm)
Đúng 1
Bình luận (0)
a)Cho (a+b)^2 = 4ab . Chứng minh rằng a=b
b)Cho (a^2+b^2)(x^2+y^2)=(ax+by)^2 . Chứng minh rằng ay=bx
a) Ta có: \(\left(a+b\right)^2=4ab\)<=> \(a^2+b^2+2ab=4ab\)
<=> \(a^2-2ab+b^2=0\)
<=> \(\left(a-b\right)^2=0\)=> a=b (đpcm)
b) Ta có: \(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
<=> \(a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+2axby+b^2y^2\)
<=> \(a^2y^2+b^2x^2-2axby=0\)
<=>\(\left(ay-bx\right)^2=0\)
<=>ay=bx(đpcm)
Đúng 0
Bình luận (0)
Chứng minh rằng: ( a + b ) 2 - ( a - b ) 2 = 4 a b . Từ đó tính: ( a + b ) 2 biết a - b = 3 và ab = 4.
Chứng minh rằng: ( a + b ) 2 - ( a - b ) 2 = 4 a b . Từ đó tính: ( a + b ) 2 biết a + b = 6 và ab = 8