Không sử dụng máy tính và nháp, hãy tính nhẩm:
\(A=10^3-3^3-7^3\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Tính nhẩm : (24 x 26 - 124) : 50
Nói trước cấm sử dụng những vật như : Giấy nháp, máy tính, bàn tính, máy tính trong điện thoại,.. để tính
Và những phương pháp : Đặt cột tính, hỏi người lớn,.. để tính
Khi trả lời nói luôn cách tính nhẩm, cách nào thông minh nhất mình sẽ tick
tách 24=4.6
26=25+1
=>24.26+24.25+24+6.4.25+24=6.100+24=600+24+624
lấy (624-124):5=500:5=100
bằng mông to và chim to nha bạn
Không sử dụng máy tính, hãy tính:
a) \({( - 3)^8}\) biết \({( - 3)^7} = - 2187\)
b) \({\left( { - \frac{2}{3}} \right)^{12}}\) biết \({\left( { - \frac{2}{3}} \right)^{11}} = \frac{{ - 2048}}{{177147}}\)
\(\begin{array}{l}a){( - 3)^8} = {( - 3)^7}.( - 3) = - 2187.( - 3) = 6561\\b){\left( { - \frac{2}{3}} \right)^{12}} = {\left( { - \frac{2}{3}} \right)^{11}}.\left( { - \frac{2}{3}} \right) = \frac{{ - 2048}}{{177147}}.\frac{{ - 2}}{3} = \frac{{4096}}{{531441}}\end{array}\)
Cho f(x)=(2x^3-21x-29)^2013.
Không sử dụng máy tính bỏ túi hãy tính f(x)
Khi :x=3√(7+√(49/8))+3√(7-√(49/8)).
Giải hộ mình vs, 3√ là căn bậc 3 nha mn......
Không sử dụng máy tính, hãy tính sin 40 0 - sin 45 0 + sin 50 0 cos 40 0 - cos 45 0 + cos 50 0 = 6 3 + 3 tan 15 ° 3 - 3 tan 15 °
Ta có: sin 40º = cos 50º ; sin 45º = cos 45º ; sin 50º = cos 40º
Do đó :
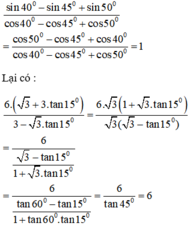
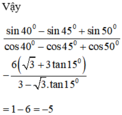
Không sử dụng máy tính cầm tay, hãy so sánh:
a) \({5^{6\sqrt 3 }}\) và \({5^{3\sqrt 6 }};\)
b) \({\left( {\frac{1}{2}} \right)^{ - \frac{4}{3}}}\) và \(\sqrt 2 {.2^{\frac{2}{3}}}.\)
a: \(6\sqrt{3}=\sqrt{108}>\sqrt{54}=3\sqrt{6}\)
\(\Rightarrow5^{6\sqrt{3}}>5^{3\sqrt{6}}\)
b: \(\sqrt{2}\cdot2^{\dfrac{2}{3}}=2^{\dfrac{1}{2}}\cdot2^{\dfrac{2}{3}}=2^{\dfrac{1}{2}+\dfrac{2}{3}}=2^{\dfrac{7}{6}}\)
\(\left(\dfrac{1}{2}\right)^{-\dfrac{4}{3}}=2^{\left(-1\right)\cdot\left(-\dfrac{4}{3}\right)}=2^{\dfrac{4}{3}}\)
mà \(\dfrac{7}{6}< \dfrac{8}{6}=\dfrac{4}{3}\).
nên \(\sqrt{2}\cdot2^{\dfrac{2}{3}}< \left(\dfrac{1}{2}\right)^{-\dfrac{4}{3}}\).
Không sử dụng máy tính cầm tay, hãy so sánh các số sau:
a) \(\sqrt {42} \) và \(\sqrt[3]{{51}}\)
b) \({16^{\sqrt 3 }}\) và \({4^{3\sqrt 2 }}\)
c) \({(0,2)^{\sqrt {16} }}\) và \({\left( {0,2} \right)^{\sqrt[3]{{60}}}}\)
\(a,\sqrt{42}=\sqrt{3\cdot14}>\sqrt{3\cdot12}=6\\ \sqrt[3]{51}=\sqrt[3]{17}< \sqrt[3]{3\cdot72}=6\\ \Rightarrow\sqrt{42}>\sqrt[3]{51}\\ b,16^{\sqrt{3}}=4^{2\sqrt{3}}\\ 18>12\Rightarrow3\sqrt{2}>2\sqrt{3}\Rightarrow4^{3\sqrt{2}}>4^{2\sqrt{3}}\\ \Rightarrow4^{3\sqrt{2}}>16^{\sqrt{3}}\)
\(c,\left(\sqrt{16}\right)^6=16^3=4^6=4^2\cdot4^4=4^2\cdot16^2\\ \left(\sqrt[3]{60}\right)^6=60^2=4^2\cdot15^2\\ 4^2\cdot16^2>4^2\cdot15^2\Rightarrow\sqrt{16}>\sqrt[3]{60}\Rightarrow0,2^{\sqrt{16}}< 0,2^{\sqrt[3]{60}}\)
Không sử dụng máy tính hãy so sánh:
A=\(\frac{19-5\sqrt{3}}{3}\)và B=2\(\sqrt{2}\)
Giả sử A > B
<=> 19 >\(5\sqrt{3}+6\sqrt{2}\)
<=> (6 + 3 - \(2\sqrt{3}\sqrt{6}\)
) + (10 - 5\(\sqrt{3}\))>0
<=> (\(\sqrt{6}-\sqrt{3}\))2 + (10 - \(5\sqrt{3}\))>0
Mà 10 - 5\(\sqrt{3}\)> 10 - 5\(\sqrt{4}\) = 0
Vậy A > B
So sánh ( Không sử dụng máy tính)
a) \(\sqrt{2}+\sqrt{3}\) và 3
b) 5 - và\(3\sqrt{2}-2\)
c) 3+ và \(2\sqrt{2}+6\)