LL
Những câu hỏi liên quan
giúp mình với
cho biểu thức A=\(\frac{x^2-2x+2011}{x^2}\)với x>0.Tìm giá trị của x để A đạt giá trị nhỏ nhất.Tìm giá trị nhỏ nhất đó
mình đg cần gấp ạ!!
Cho A= 3x2 + 18x + 33
a) Chứng minh A> 0 với mọi giá trị của x
b) Tìm giá trị nhỏ nhất của A
Giúp mình với!!!!
a, A = 3x2 + 18x + 33 => 3A = 9x2 + 54x + 99 = (3x)2 + 2.3x.9 + 81 + 18 = (3x + 9)2 + 18
Vì (3x + 9)2 > hoặc = 0 với mọi x => (3x + 9)2 + 18 luôn > 0 => 3A > o với mọi x hây > 0 với mọi x.
b, Ta có 3A = (3x + 9)2 + 18.
Vì (3x + 9)2 > hoặc = 0 với mọi x => (3x + 9)2 + 18 > hoặc = 18
Do đó 3A > hoặc = 18 => A > hoặc = 6.
Dấu = xảy ra <=> (3x + 9)2 = 0
<=> 3(x + 3) = 0
<=> x + 3 = 0
<=> x = -3
Vậy GTNN của A = 6 khi x = -3
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của A:
A=(x+4)2020+17
SOS
Giải giúp mình với ạ
Ta thay x bằng số -4. Khi đó -4+4=0, mà 0 mũ 2020 thì vẫn bằng 0. 0+17=17. Đáp án: 17
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của A= x^2 - 3x + 2 Giúp mình với ạ, mình cảm ơn
\(A=x^2-3x+2\\ \Rightarrow A=\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{1}{4}\\ \Rightarrow A=\left(x-\dfrac{3}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{3}{2}\)
Vậy \(A_{min}=-\dfrac{3}{4}\Leftrightarrow x=\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
cho bốn số dương a,b,c,d. Tìm giá trị nhỏ nhất của biểu thức :
\A=a/b+c + b/c+d +c/d+a + d/a+b
mọi người giải giúp mình với ạ
Chú ý rằng vì
x
+
a
2
≥
0
với mọi giá trị của x và
x
+
a
2
0
khi x -a nên
x
+
a
2
+
b
≥
0...
Đọc tiếp
Chú ý rằng vì x + a 2 ≥ 0 với mọi giá trị của x và x + a 2 = 0 khi x = -a nên x + a 2 + b ≥ 0 với mọi giá trị của x và x + a 2 + b = b khi x = -a .Áp dụng điều này giải các bài tập sau:
Rút gọn rồi tìm giá trị của x để biểu thức x 2 x - 2 . x 2 + 4 x - 4 + 3 có giá trị nhỏ nhất. Tìm giá trị nhỏ nhất ấy.
Điều kiện x ≠ 2 và x ≠ 0
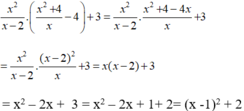
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.
Đúng 0
Bình luận (0)
Mọi người ai giúp mình giải bài này với ạ. Ai biết rõ cách trình bày thì càng tốt nha! Cảm ơn nhiều ạ!
Đề bài: Tìm giá trị nhỏ nhất của biểu thức:
A=\(\frac{x^2-3x+3}{x^2-2x+1}\)
* mọi người giúp mình 2 bài này với ạ*Bài 8: Cho phương trình (a2 - 4)x -12x + 7 0 (a là tham số)a) Giải phương trình với a 1b) Tìm các giá trị của a sao cho phương trình nhận x 1 là nghiệm.c) Tìm điều kiện của a để phương trình đã cho luôn có một nghiệm duy nhấtBài 9: Giải và biện luận phương trình ẩn x theo tham số ma) (m2 - 9)x - m + 3 0b)dfrac{x+3}{x-1}dfrac{x+m}{x+1}
Đọc tiếp
* mọi người giúp mình 2 bài này với ạ*
Bài 8: Cho phương trình (a2 - 4)x -12x + 7 = 0 (a là tham số)
a) Giải phương trình với a = 1
b) Tìm các giá trị của a sao cho phương trình nhận x = 1 là nghiệm.
c) Tìm điều kiện của a để phương trình đã cho luôn có một nghiệm duy nhất
Bài 9: Giải và biện luận phương trình ẩn x theo tham số m
a) (m2 - 9)x - m + 3 = 0
b)\(\dfrac{x+3}{x-1}=\dfrac{x+m}{x+1}\)
Bài 8:
a: Khi a=1 thì phương trình sẽ là \(\left(1-4\right)x-12x+7=0\)
=>-3x-12x+7=0
=>-15x+7=0
=>-15x=-7
hay x=7/15
b: Thay x=1 vào pt, ta được:
\(a^2-4-12+7=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+3\right)=0\)
hay \(a\in\left\{3;-3\right\}\)
c: Pt suy ra là \(\left(a^2-16\right)x+7=0\)
Để phương trình đã cho luôn có một nghiệm duy nhất thì (a-4)(a+4)<>0
hay \(a\notin\left\{4;-4\right\}\)
Đúng 0
Bình luận (0)
**giúp mình với các bạn mình đang cần gấp***
toán cực trị lớp 8
cho a>0, b>0 và a+b = 3
a) tìm giá trị nhỏ nhất của N=a2+b2
b) tìm giá trị lớn nhất của P=ab+2
a)Áp dụng BĐT bunhiacoxki ta có: \(\left(a^2+b^2\right)\left(1^2+1^2\right)\ge\left(a.1+b.1\right)^2=\left(a+b\right)^2=3^2=9\)
=>\(2\left(a^2+b^2\right)\ge9\Leftrightarrow a^2+b^2\ge\frac{9}{2}\)
Dấu "=" xảy ra khi: a=b
Vậy GTNN của N là 9/2 tại a=b
b)Ta có: \(a^2+b^2\ge\frac{9}{2}\) (câu a)
<=>(a+b)2-2ab\(\ge\frac{9}{2}\)
<=>\(9-2ab\ge\frac{9}{2}\)
<=>\(2ab\le\frac{9}{2}\)
<=>\(ab\ge\frac{9}{4}\)
<=>\(ab+2\le\frac{17}{4}\)
Dấu "=" xảy ra khi a=b
Vậy GTLN của P là 17/4 tại a=b
Đúng 0
Bình luận (0)



