65*x^6 -2*x^3 *y + y^2 = 64
DD
Những câu hỏi liên quan
Tìm x,y,z :
a , 3/2x = 4/5y = 6/7z và x- y -2z= -45
b , x/2 = y/3 = z/4 và x^2 - y^2 + 2z^2=108
c, x^3 /8 = y^3/64 = z^3/216 và x^2 + y ^2 + z^2 = 14
b) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k\\y=3k\\z=4k\end{matrix}\right.\)
Ta có: \(x^2-y^2+2z^2=108\)
\(\Leftrightarrow\left(2k\right)^2-\left(3k\right)^2+2\cdot\left(4k\right)^2=108\)
\(\Leftrightarrow4k^2-9k^2+2\cdot16k^2=108\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k=2\cdot2=4\\y=3k=3\cdot2=6\\z=4k=4\cdot2=8\end{matrix}\right.\)
Trường hợp 2: k=-2
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k=2\cdot\left(-2\right)=-4\\y=3k=3\cdot\left(-2\right)=-6\\z=4k=4\cdot\left(-2\right)=-8\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm X,Y biết \(\frac{x^3+y^3}{6}=\frac{x^3-2y^2}{4}vàx^6\times y^6=64\)
x6.y6=64 (x,y khác 0)
<=> (x.y)6=26 (64=26)
=> x.y=2 => x=2/y
Lại có: \(\frac{x^3+y^3}{6}=\frac{x^3-2y^2}{4}\) <=> \(\frac{x^3+y^3}{3}=\frac{x^3-2y^2}{2}\)
<=> 2x3+2y3=3x3-6y2
<=> 2y3=x3-6y2 . Thay x=y/2 vào ta được:
\(2y^3=\frac{y^3}{8}-6y^2\) <=> 16y3=y3-48y2
<=> 15y3+48y2 =0
<=> y2(15y+48)=0
Do y khác 0 => 15y+48=0 => \(y=-\frac{48}{15}=-\frac{16}{5}\)
x=y/2 => \(x=-\frac{8}{5}\)
Đáp số: \(x=-\frac{8}{5}\); \(y=-\frac{16}{5}\)
Đúng 0
Bình luận (0)
cho x mũ 3 cộng y mũ 3 phần 6 bằng x mũ 3 trừ 2 y mũ 3 phần 4 và x mũ 6 nhân y mũ 6 =64
Tìm x,y biết:
\(\frac{x^3+y^3}{6}=\frac{x^3-2\cdot y^3}{4}\)và \(x^6+y^6=64\)
\(\frac{x^3+y^3}{6}=\frac{x^3-2y^3}{4}\Leftrightarrow4x^3+4y^3=6x^3-12y^3\)
\(\Leftrightarrow4x^3+16y^3=6x^3\Leftrightarrow2x^3=16y^3\Leftrightarrow x^3=8y^3\Leftrightarrow x=2y\)
\(\Rightarrow x^6+y^6=65\left(y^6\right)=64\Leftrightarrow y^6=\frac{64}{65}\)
\(\Rightarrow y=\frac{\sqrt[6]{64}}{\sqrt[6]{65}}\Rightarrow x=\frac{2\sqrt[6]{64}}{\sqrt[6]{65}}\)
Đúng 0
Bình luận (0)
phân tích đa thức sau thành nhân tử :
(3x+1)^2 - 4(x - 2 )^2
9(2x+3)^2 - 4(x+1)^2
8x^3 - 64
x^6 - y^6
(x+y)^3 - (x - y )^3
\(\left(3x+1\right)^2-4\left(x-2\right)^2=9x^2+6x+1-4\left(x^2-4x+4\right)=9x^2+6x+1-4x^2+16x-16=5x^2+22x-15=\)
\(\left(5x-3\right)\left(x+5\right)\)
Đúng 0
Bình luận (0)
\(9\left(2x+3\right)^2-4\left(x+1\right)^2=9\left(4x^2+12x+9\right)-4\left(x^2+2x+1\right)=36x^2+108x+81-4x^2-8x-4=32x^2+100x+77\)
\(\left(8x+11\right)\left(4x+7\right)\)
Đúng 0
Bình luận (0)
\(8x^3-64=\left(2x\right)^3-4^3=\left(2x-4\right)\left(4x^2+8x+16\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
2 ( x - y ) + (x - y )mũ 2 + ( y - x ) mũ 2 tại x = -3 , y = 1000
x mũ 3 + 12x mũ 2 + 48x + 64 tại x = 6
x mũ 3 - 6x mũ 2 + 12x - 8 tại x = 22
1) Ta có: \(2\left(x-y\right)+\left(x-y\right)^2+\left(y-x\right)^2\)
\(=2\left(-3-1000\right)+\left(-3-1000\right)^2+\left(3+1000\right)^2\)
\(=-2006+1006009+1006009\)
\(=2010012\)
2) \(x^3+12x^2+48x+64\)
\(=x^3+3.x^2.4+3.x.4^2+4^3\)
\(=\left(x+4\right)^3=\left(6+4\right)^3=10^3=1000\)
3) \(x^3-6x^2+12x-8\)
\(=x^3-3.x^2.2+3.x.2^2-2^3\)
\(=\left(x-2\right)^3=\left(22-2\right)^3=20^3=8000\)
\(2\left(x-y\right)+\left(x-y\right)^2+\left(y-x\right)^2\)
=\(2\left(x-y\right)+\left(x-y+y-x\right)\left(x-y-\left(y-x\right)\right)\)
= \(2\left(x-y\right)+\left(x-y+y-x\right)\left(x-y-y+x\right)\)
= \(2\left(x-y\right)\)
Thay x = -3,y = 1000 vào ta có : 2(x - y) = 2(-3 - 1000) = 2.(-1003) = -2006
\(x^3+12x^2+48x+64\)
\(=x^3+3\cdot x^2\cdot4+3\cdot x\cdot4^2+4^3=\left(x+4\right)^3\)
Thay x = 6 vào ta có : (6 + 4)3 = 103 = 10000
\(x^3-6x^2+12x-8=x^3-3x^2\cdot2+3x\cdot2^2-2^3\)
\(=\left(x-2\right)^3\)
Thay x = 22 vào ta có : (22 - 2)3 = 203 = 8000
a) 2( x - y ) + ( x - y )2 + ( y - x )2
= 2( x - y ) + ( x - y )2 + ( x - y )2
= ( x - y )[ 2 + ( x - y ) + ( x - y ) ]
= ( x - y )( 2 + x - y - x - y )
= ( x - y )( 2x - 2y + 2 )
= 2( x - y )( x - y + 1 )
Thế x = -3 ; y = 1000 ta được
2( -3 - 1000 )( -3 - 1000 + 1 ) = 2010012
b) x3 + 12x2 + 48x + 64 = ( x + 4 )3
Thế x = 6 ta được ( 6 + 4 )3 = 103 = 1000
c) x3 - 6x2 + 12x - 8 = ( x - 2 )3
Thế x = 22 ta được ( 22 - 2 )3 = 203 = 8000
Xem thêm câu trả lời
Bài 1 : Tìm x ,y,z biết:
a, 3/x-1 = 4/y-2 = 5/z-3 và x+y+z = 18
b, 3/x-1 = 4/y-2 = 5/z-3 và x.y.z = 192
Bài 2 : Tìm x,y,z biết : x^3+y^3/6 = x^3-2y^3/4 và x^6.y^6 = 64
Bài 3 : Tìm x,y,z biết :x+4/6 = 3y-1/8 = 3y-x-5/x
Bài 4 :Tìm x,y,z biết : x+y+2005/z = y+z-2006 = z+x+1/y = 2/x+y+z
bài 1 : a,ta có 3/x-1 =4/y-2=5/z-3 => x-1/3=y-2/4=z-3/5
áp dụng .... => x-1+y-2+z-3 / 3+4+5 = x+y+z-1-2-3/3+4+5 = 12/12=1
do x-1/3 = 1 => x-1 = 3 => x= 4 ( tìm y,z tương tự
Đúng 2
Bình luận (0)
Bài 1:
a) Ta có: 3/x - 1 = 4/y - 2 = 5/z - 3 => x - 1/3 = y - 2/4 = z - 3/5 áp dụng ... =>x - 1 + y - 2 + z - 3/3 + 4 + 5 = x + y + z - 1 - 2 - 3/3 + 4 + 5 = 12/12 = 1 do x - 1/3 = 1 => x - 1 = 3 => x = 4 ( tìm y, z tương tự )
cũng dễ thôi
Xem thêm câu trả lời
Vẽ các hypebol sau:
a) \(\frac{{{x^2}}}{{10}} - \frac{{{y^2}}}{6} = 1\)
b) \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 - y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:

b) Nhập phương trình hypebol theo cú pháp x^2/4 - y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
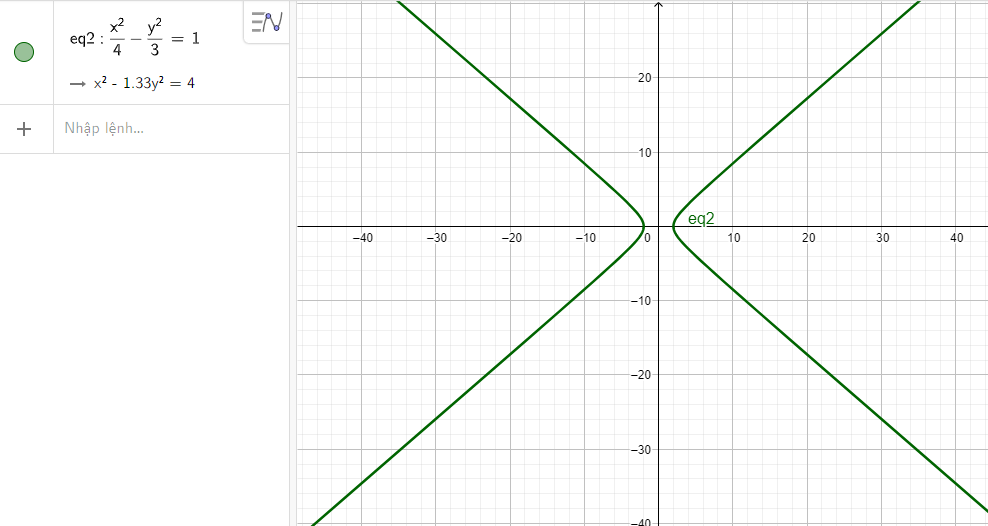
c) Nhập phương trình hypebol theo cú pháp x^2/64 - y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:

Đúng 0
Bình luận (0)
A) (X-3/5)^2=64
B) x/4=y/6, y/2=z/3 và y+x+z= 121
a) (\(x-\dfrac{3}{5}\))\(^2\)=64
=> \(x-\dfrac{3}{5}\)=\(\sqrt{64}\)
=> \(x-\dfrac{3}{5}\) =8 hoặc \(x-\dfrac{3}{5}\)=-8
Trường hợp 1:
\(x-\dfrac{3}{5}\) = 8=>\(x\) =\(8+\dfrac{3}{5}\)=>\(x\)=\(\dfrac{43}{5}\)
Trường hợp 2:
\(x-\dfrac{3}{5}\)=\(-8\)=>\(x\)=\(-8+\dfrac{3}{5}\)=>\(x=-\dfrac{37}{5}\)
Đúng 0
Bình luận (0)
b: y/2=z/3 nên y/6=z/9
=>x/4=y/6=z/9=(x+y+z)/(4+6+9)=121/19
=>x=484/19; y=726/19; z=1089/19
Đúng 0
Bình luận (0)



