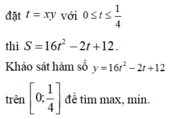Với x>0 tìm giá trị nhỏ nhất của M = 4x2-3x+\(\frac{1}{x+4}\)+2019
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NL
Những câu hỏi liên quan
Cho
0
≤
x
;
y
≤
1
thỏa mãn
2017
1
−
x
−
y
x
2
+
2018
x
2
−
2
y
+...
Đọc tiếp
Cho 0 ≤ x ; y ≤ 1 thỏa mãn 2017 1 − x − y = x 2 + 2018 x 2 − 2 y + 2019 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức S = 4 x 2 + 3 y 4 y 2 + 3 x + 25 x y . Khi đó M + m bằng bao nhiêu?
A. 136 3
B. 391 16
C. 383 16
D. 25 2
Đáp án B
Từ giả thiết
2017 1 − y 2017 x = x 2 + 2018 1 − y 2 + 2018 ⇔ 2017 1 − y 1 − y 2 + 2018 = 2017 x x 2 + 2018 *
Xét hàm số f t = 2017 t t 2 + 2018 với t ∈ 0 ; 1
⇒ f ' t = 2017 t ln 2017 t 2 + 2018 + 2 t .2017 t > 0
⇒ f t đồng biến trên 0 ; 1 . Do đó (*) ⇔ 1 − y = x ⇔ x + y = 1.
Ta có: 0 ≤ x y ≤ x + y 2 4 = 1 4 . Đặt m = x y ∈ 0 ; 1 4 . Khi đó :
S = 16 x 2 y 2 + 34 x y + 12 y + x y + x 2 − 3 x y = 16 m 2 − 2 m + 12 = g m
Xét hàm g m trên đoạn
0 ; 1 4 ⇒ g ' m = 32 m − 2 → g ' m = 0 ⇔ m = 1 16
Lúc này
g 0 = 12 , g 1 4 = 25 2 , g 1 16 = 191 16 ⇒ M = 25 2 m = 191 16 ⇒ M + m = 391 16 .
Đúng 0
Bình luận (0)
Cho
0
≤
x
;
y
≤
1
thỏa mãn
2017
1
-
x
-
y
x
2
+
2018
x
2
-...
Đọc tiếp
Cho 0 ≤ x ; y ≤ 1 thỏa mãn 2017 1 - x - y = x 2 + 2018 x 2 - 2 y + 2019 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức S = (4x2 + 3y)(4y2 + 3x) + 25xy. Khi đó M + m bằng bao nhiêu?
![]()
![]()
![]()
![]()
Đáp án B
Từ giả thiết
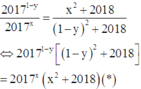
Xét hàm số
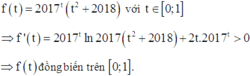
Do đó (*)
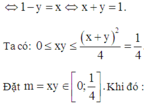
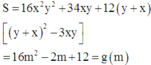
Xét hàm g(m) trên đoạn
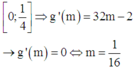
Lúc này
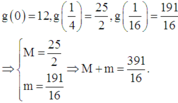
Đúng 0
Bình luận (0)
Với x>0 tìm giá trị nhỏ nhất của M = 4x2-3x+\(\frac{1}{4x}\)+2019
Cho
0
≤
x
,
y
≤
1
thỏa mãn
2017
1
-
x
-
y
x
2
+
2018
y
2...
Đọc tiếp
Cho 0 ≤ x , y ≤ 1 thỏa mãn 2017 1 - x - y = x 2 + 2018 y 2 - 2 y + 2019 . Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức S = 4 x 2 + 3 y 4 y 2 + 3 x Khi đó M+m bằng bao nhiêu?
A. 383 16
B. 136 3
C. 25 2
D. 391 16
Cho
0
≤
x
,
y
≤
1
thỏa mãn
2017
1
−
x
−
y
x
2
+
2018
y
2
−
2
y
+...
Đọc tiếp
Cho 0 ≤ x , y ≤ 1 thỏa mãn 2017 1 − x − y = x 2 + 2018 y 2 − 2 y + 2019 . Gọi M,mlần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức S = 4 x 2 + 3 y 4 y 2 + 3 x + 25 x y . Khi đó M + m bằng bao nhiêu?
A. 136/3
B. 391/16
C. 383/16
D. 25/2
Đáp án B
Ta có 2017 1 − x − y = x 2 + 2018 y 2 − 2 y + 2019 ⇔ 2017 1 − y 2017 x = x 2 + 2018 1 − y 2 + 2018
2017 x x 2 + 2018 = 2017 1 − y 1 − y 2 + 2018 ⇔ f x = f 1 − y
Xét hàm số f t = 2017 t t 2 + 2018 = t 2 .2017 t + 2018.2017 t , có
f ' t = 2 t .2017 t + t 2 .2017 t . ln 2017 + 2018.2017 t . ln 2017 > 0 ; ∀ t > 0
Suy ra f(t) là hàm đồng biến trên 0 ; + ∞ mà f x = f 1 − y ⇒ x + y = 1
Lại có P = 4 x 2 + 3 y 4 y 2 + 3 x + 25 x y = 16 x 2 y 2 + 12 x 3 + 12 y 3 + 34 x y
16 x 2 y 2 + 12 x + y 3 − 3 x y x + y + 34 x y = 16 x 2 y 2 + 12 1 − 3 x y + 34 x y = 16 x 2 y 2 − 2 x y + 12
Mà 1 = x + y ≥ 2 x y ⇔ x y ≤ 1 4 nên đặt t = x y ∈ 0 ; 1 4 khi đó P = f t = 16 t 2 − 2 t + 12
Xét hàm số f t = 16 t 2 − 2 y + 12 trên 0 ; 1 4 ta được min 0 ; 1 4 f t = f 1 16 = 191 16 max 0 ; 1 4 f t = f 1 4 = 25 2
Đúng 0
Bình luận (0)
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức
S
(
4
x
2
+
3
y
)
(
4
y
2
+
3
x
)
+
25
x
y
là: A.
M
25
2
;
m...
Đọc tiếp
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y=1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức S = ( 4 x 2 + 3 y ) ( 4 y 2 + 3 x ) + 25 x y là:
A. M = 25 2 ; m = 191 16 .
B. M = 12 ; m = 191 16 .
C. M = 25 2 ; m = 12 .
D. M = 25 2 ; m = 0 .
Do x+ y= 1 nên
S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y , d o x + y = 1 = 16 x 2 y 2 - 2 x y + 12
Đặt t= xy . Do x≥ 0 ; y≥0 nên
0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4
Xét hàm số f(t) = 16t2- 2t + 12 trên [0 ; 1/4].
Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16 .
Bảng biến thiên
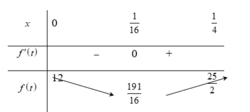
Từ bảng biến thiên ta có:
m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ; m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2
Vậy giá trị lớn nhất của S là 25/2 đạt được khi
x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2
giá trị nhỏ nhất của S là 191/ 16 đạt được khi
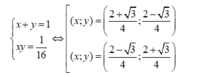
Chọn A.
Đúng 0
Bình luận (0)
Bài 1: Tìm giá trị nhỏ nhất của biểu thức [(x+1/2)2 + 5/4]
Bài 2: Cho đa thức M= x3+x2y-3x2-xy-y2+4y+x+2019
Tính giá trị của đa thức M biết x+y-3=0
Bài 1:
Ta thấy: $(x+\frac{1}{2})^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow (x+\frac{1}{2})^2+\frac{5}{4}\geq \frac{5}{4}$
Vậy gtnn của biểu thức là $\frac{5}{4}$
Giá trị này đạt tại $x+\frac{1}{2}=0\Leftrightarrow x=-\frac{1}{2}$
Đúng 0
Bình luận (0)
Bài 2:
$x+y-3=0\Rightarrow x+y=3$
\(M=x^2(x+y)-(x+y)x^2-y(x+y)+4y+x+2019\)
\(=-3y+4y+x+2019=x+y+2019=3+2019=2022\)
Đúng 1
Bình luận (1)
Tìm giá trị nguyên của x để:
B=\(\frac{2019x-2019}{3x+2}\)có giá trị nhỏ nhất
Với x>0 , tìm giá trị nhỏ nhất của biểu thức : \(M=4x^2-3x+\frac{1}{4x}+2011\)
\(M=\)như trên
\(=>M=4x^2-4x+1+x+\frac{1}{4x}+2010\)
\(=>M=\left(4x^2-4x+1\right)+\left(x+\frac{1}{4x}\right)+2010\)
\(=>M=\left(2x-1\right)^2+\left(x+\frac{1}{4x}\right)+2010\)
Áp dụng BĐT Cô- si cho 2 số không âm, ta có:
\(x+\frac{1}{4x}\ge2\sqrt{x.\frac{1}{4x}}=2\sqrt{\frac{1}{4}}=1\)
\(=>M=\left(2x-1\right)^2+\left(x+\frac{1}{4x}\right)+2010\ge0+1+2010=2011\\ \)
=>minM=2011 khi x=\(\frac{1}{2}\)