a, Có hay không :
Nếu x>0,y<0 thì : x2+√x+y2−y2≥x2y
b, |x+2018|y −2018y2≤2018
xy≥0;x+2y =314
Bài cực khó nếu ai làm đúng thì mik thick cho
Câu hỏi tương tự Đọc thêm Báo cáo
NM
Những câu hỏi liên quan
Nếu x < 0 , y < 0 thì căn bậc hai của xy có phải không xác định hay không ?
\(\sqrt{xy}\)vẫn xác định khi \(x< 0;y< 0\)(khi đó \(xy>0\)), nhưng đừng bao giờ viết \(\sqrt{xy}=\sqrt{x}.\sqrt{y}\)
Cho hàm số y=f(x) liên tục trên đoạn [a; b]. Nếu f(a).f(b) > 0 thì phương trình f(x) = 0 có nghiệm hay không trong khoảng (a; b)? Cho ví dụ minh hoạ.
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Ví dụ minh hoạ :
- f ( x ) = x 2 − 1 liên tục trên đoạn [−2;2], f(−2).f(2) = 9 > 0
Phương trình x 2 – 1 = 0 có nghiệm x = 1 hoặc x = -1 trong khoảng (-2; 2)
- f ( x ) = x 2 + 1 liên tục trên đoạn [-1; 1] và f(−1).f(1) = 4 > 0. Còn phương trình x 2 + 1 = 0 lại vô nghiệm trong khoảng (-1; 1)
Đúng 0
Bình luận (0)
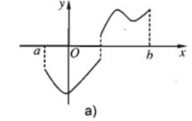
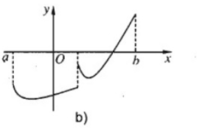
Nếu hàm số y = f(x) không liên tục trên đoạn [a; b] nhưng f(a).f(b) < 0 thì phương trình f(x) = 0 có nghiệm hay không trong khoảng (a; b)? Hãy giải thích câu trả lời bằng minh hoạ hình học.
Nếu hàm số y = f(x) không liên tục trên đoạn [a; b] nhưng f(a).f(b) < 0 thì phươngtrình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Minh hoạ hình hoạ (H.8):
Đúng 0
Bình luận (0)
Cho 5 số tự nhiên khác 0 và a ; b ; x ; y ; z thỏa mãn
a^2 + b^2 = x^2 + y^2 + z^2 .Hỏi tổng S có là số
nguyên tố hay không nếu S = a + b + x + y + z
1. Tìm các số nguyên x biết: (x+3).(x-4)<0
2. Có hay không các số nguyên x và y ( nếu không thì giải thích vì sao)
x.y.(x+y)=-456789
HELF ME!!!!!!!!!!!!!!!!!
a, Có hay không :
Nếu x>0,y<0 thì : \(x^2\)+\(\sqrt{x+y^2}-y^2\)\(\ge x^2y\)
b, \(\frac{\left|x+2018\right|}{y}-2018y^2\le2018\)
\(xy\ge0;\frac{x+2}{y}=314\)
Bài cực khó nếu ai làm đúng thì mik thick cho
Ý kiến sau đúng hay sai ?
"Nếu hàm số y = f(x) liên tục tại điểm x0 còn hàm số y = g(x) không liên tục tại x0, thì
y = f(x) + g(x) là một hàm số không liên tục tại x0."
Ý kiến đúng
Giả sử ngược lại y = f(x) + g(x) liên tục tại x0. Đặt h(x) = f(x) + g(x). Ta có g(x) = h(x) - f(x).
Vì y = h(x) và y = f(x) liên tục tại x0 nên hiệu của chúng là hàm số y = g(x) phải liên tục tại x0. Điều này trái với giả thiết là y = g(x) không liên tục tại x0.
Đúng 0
Bình luận (0)
x, y có là số vô tỉ hay không nếu x+y và x/y là số hữu tỉ
Xem thêm câu trả lời
Cho 2 phương trình x^2 + 2015x - 2016 = 0 và y^2 + 2015y - 2016 = 0.
Không giải phương trình có cách nào tính được x - y, x + y hay không? Biết rằng x > y.
Nhìn là biết đáp án x-y=0 và x+y=2 mà bạn. Do x=1, y=1
Đúng 0
Bình luận (0)
Cho hàm số \(y=f\left(x\right)\) liên tục trên đoạn [a; b]. Nếu \(f\left(a\right).f\left(b\right)>0\) thì phương trình \(f\left(x\right)=0\) có nghiệm hay không trong khoảng (a;b) ? Cho ví dụ minh họa ?
