cho tam giác ABC cân ở A có AB=17cm,BC=16cm. Kẻ trung tuyến AM.
CMR:
a) AM _I_ BC
b) Tính độ dài AM
Cho tam giác cân ở A có AB=AC=17cm,BC=16cm. Kẻ trung tuyến AM. Cm rằng:
a, AM (vuông góc) BC
b, Tính độ dài AM
Cho tam giác ABC cân tại A, AB = 17cm, BC = 16cm. Kẻ trung tuyến AM. Gọi G là trọng tâm của tam giác ABC. Chứng minh: a) AM BC b) Tính độ dài AG, GM
Gíup mik zới ạ
tham khảo
+ Vì MAM là đường trung tuyến của ΔABC(gt)ΔABC(gt)
=> MM là trung điểm của BC.BC.
=> BM=CM=12BCBM=CM=12BC (tính chất trung điểm).
=> BM=CM=12.16=162=8(cm).BM=CM=12.16=162=8(cm).
+ Xét ΔABCΔABC có:
AB=AC=17cm(gt)AB=AC=17cm(gt)
=> ΔABCΔABC cân tại A.A.
Có AMAM là đường trung tuyến (gt).
=> AMAM đồng thời là đường cao của ΔABC.ΔABC.
=> AM⊥BC.AM⊥BC.
+ Xét ΔABMΔABM vuông tại M(cmt)M(cmt) có:
AM2+BM2=AB2AM2+BM2=AB2 (định lí Py - ta - go).
=> AM2+82=172AM2+82=172
=> AM2=172−82AM2=172−82
=> AM2=289−64AM2=289−64
=> AM2=225AM2=225
=> AM=15(cm)AM=15(cm) (vì AM>0AM>0).
+ Vì G là trọng tâm của ΔABC(gt).ΔABC(gt).
=> AG=23AMAG=23AM (tính chất trọng tâm của tam giác).
=> AG=23.15AG=23.15
=> AG=303AG=303
=> AG=10(cm).AG=10(cm).
Vậy AM=15(cm);AG=10(cm).
Bài 2: Cho tam giác ABC cân tại A có AB = AC = 5cm, BC = 3cm. Kẻ trung tuyến AM.
a) Chứng minh rằng AM vuông góc với BC
b) Tính độ dài AM.
a, Xét tam giác ABC cân tại A có AM là trung tuyến
=> AM đồng thời là đường cao => AM vuông BC
b, Ta có BM = BC/2 = 3/2 cm
Theo định lí Pytago tam giác AMB vuông tại M
\(AM=\sqrt{AB^2-BM^2}=\dfrac{\sqrt{91}}{2}cm\)
Câu 1. Cho tam giác ABC có góc B =90 độ , vẽ trung tuyến AM . Trên tia đối của tia AM lấy điểm E sao cho ME=AM . C/m rằng :
a. Tam giác ABM=tam giác ECM
b. AC>CE
c. Góc BAM > góc MAC
Câu 2. Cho tam giác ABC cân ở A có AB=AC=17cm ; BC=16cm .Kẻ trung tuyến AM .C/m rằng :
a.AM vuông góc BC
b.Tính độ dài AM
Câu 3. Cho tam giác nhọn nhọn ABC , hai đường cao BM,CN . Trên tia đối của tia BM lấy điểm D sao cho BD =AC, trên tia đối của tia CN lấy điểm E sao cho CE=AB . C/m :
a. góc ACE = góc ABD
b. Tam giác ACE = tam giác DBA
c. Tam giác AED là tam giác vuông cân
Tam giác ABC cân tại A có AB = AC = 34cm, BC = 32cm. Kẻ đường trung tuyến AM. Tính độ dài AM
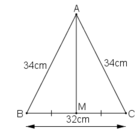
Do M là trung điểm của BC nên BM = CM = BC/2 cm
Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).
Cho tam giác ABC cân tại A, A B = 10 c m , B C = 16 c m . Độ dài đường trung tuyến AM là:
A. 6cm
B. 156 c m
C. 2cm
D. 4cm
Tam giác ABC cân tại A nên AM đồng thời là đường cao và M là trung điểm của BC
Khi đó ta có AM2 = AB2 - BM2 = 102 - 82 = 36 ⇒ AM = 6cm. Chọn A
Cho tam giác ABC có AB=AC=10cm; BC=16cm. Trung tuyến AM. Chứng Minh rằng : A) Tam giác ABM= Tam giác AC B) AM vuông góc BC C) Tính độ dài AM
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BM=CM=BC/2=8(cm)
nên AM=6(cm)
tham khảo
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BM=CM=BC/2=8(cm)
nên AM=6(cm)
a, Ta có :
AB = AC (gt)
=> Δ ABC cân tại A
Xét Δ ABM và Δ ACM, có :
AB = AC (gt)
MB = MC (M là trung điểm BC)
\(\widehat{ABM}=\widehat{ACM}\) (Δ ABC cân tại A)
=> Δ ABM = Δ ACM
b, Ta có :
AM là đường trung tuyến
Δ ABC cân tại A
=> AM ⊥ BC
c, Ta có :
BC = 2MB
=> 16 = 2MB
=> MB = 8 (cm)
Xét Δ AMB vuông tại M, có :
\(AB^2=AM^2+BM^2\)
=> \(10^2=AM^2+8^2\)
=> \(AM^2=36\)
=> AM = 6 (cm)
cho tam giác ABC cân tại A có AB=AC = 17cm; BC=16cm.kẻ trung tuyến AM .CMR a, AM vuông góc với BC , b, tính Am
Bài 1. Cho tam giác ABC cân tại A. Kẻ AM vuông góc với BC tại M
a) Chứng minh AM là trung tuyến của tam giác
b) Biết AB = 15 cm; BC = 12 cm. Tính độ dài đường trung tuyến AM.