Câu 11.4 trang 28 Sách Bài Tập (SBT) Toán lớp 6 tập 2
Chứng tỏ rằng 1/101+1/102+...+1/299+1/300>23
Câu 11.6 trang 28 Sách Bài Tập (SBT) Toán lớp 6 tập 2
Chứng tỏ rằng 1/5+1/6+1/7+...+1/17<2
Áp dụng công thức : \(\frac{1}{a+1}+\frac{1}{a}< 1\).Ta có:
\(\frac{1}{5}+\frac{1}{6}< 1\)
\(\frac{1}{6}+\frac{1}{7}< 1\)
. . . . .
\(\frac{1}{16}+\frac{1}{17}< 1\)
_______________________________________
\(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+...+\frac{1}{17}< 1-\frac{1}{17}\)
\(\Rightarrow\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+...+\frac{1}{17}< 1\). Vì 1 < 2 nên:
\(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+...+\frac{1}{17}< 2^{\left(đpcm\right)}\)
P/s: đpcm nghĩa là Điều phải chứng minh nha
giải bài 25 SBT toán hình 6 tập 2 trang 89 ( nhớ là sách bài tập toán tập 2 hình trang 89 lớp 6 nhé )
mik hiểu rùi ko cần trả lời nữa đâu
Bình Ngô đại cáo ra đời vào năm nào?
Năm 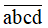
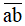 gấp đôi số ngày trong một tuần lễ, còn
gấp đôi số ngày trong một tuần lễ, còn 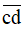 gấp đôi của
gấp đôi của 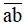 . Tính xem năm đó là năm nào.
. Tính xem năm đó là năm nào.
Số ngày trong một tuần lễ là 7 ngày thì gấp đôi số ngày trong một tuần lễ là 14.
Suy ra = 14.
Gấp đôi là 14.2 = 28.
Vì gấp đôi của nên = 28.
Vậy năm đó là năm 1428.
Bạn ht
Chứng tỏ rằng 1/101+1/102+....+1/299+1/300>2/3
chứng tỏ rằng 1/101+1/102+........+1/299+1/300>2/3
Tra lời:
Ta có:
1/101➢1/300+1/102➢1/300+1/103➢1/300+1/104➢1/300+.....+1/299➢1/300
=1/101+1/102+1/103+...1/299➢199/300
=1/101+1/102+1/103+...1/299+1/300➢199/300+1/300
=200/300=2/3.
Note: ➢ là dau lớn do nhe. Nho tick cho minh nha😊😉
Bài 52 phần C SBT tập 1 trang 20 Toán Lớp 6
chứng tỏ rằng 1/101+1/102+...+1/299+1/300>2/3
\(\frac{1}{101}\)\(+\)\(\frac{1}{102}\)\(+\). . . . \(+\)\(\frac{1}{299}\)\(+\)\(\frac{1}{300}\)\(\ge\)\(\frac{2}{3}\)\(\ge\)\(\frac{1}{300}\)\(+\)\(\frac{1}{300}\)\(+\)\(\frac{1}{300}\)\(=\)\(\frac{200}{300}\)\(=\)\(\frac{2}{3}\)
do \(\frac{1}{101}\)..... \(\frac{1}{300}\)có 200 số
\(\Rightarrow\)\(\frac{1}{101}\)\(+\)\(\frac{1}{102}\)\(+\)..... \(+\)\(\frac{1}{299}\)\(+\)\(\frac{1}{300}\)\(\ge\)\(\frac{1}{300}\)\(\times\)200
\(\ge\)\(\frac{2}{3}\)
Câu 1: Tính tích P = ( 1 - 1/2 ) x ( 1 - 1/4 )....
( 1 - 1/99 ).
Câu 2: Chứng tỏ rằng 1/101 + 1/102 +....+ 1/299 + 1/300 > 2/3.
ai có sách bài tập toán lớp 7 giải giúp minh 2 bài này kiểu tự luận nhé ko phải khoanh
bai I.9 trang 116
bai I.10 trang 116
sbt toán 7 tập 1 giúp minh nhé mình tích cho cảm ơn :))