Tìm ba số tự nhiên a;b;c khác nhau và khác 0 thỏa mãn:
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1\)
Cho hai số tự nhiên 99;100. Hãy tìm số tự nhiên a để ba số có được tạo thành ba số tự nhiên liên tiếp
A. 98
B. 97
C. 101
D. Cả A, C đều đúng
Đáp án cần chọn là: D
Số liền trước số 99 là 98 nên ba số tự nhiên liên tiếp là 98;99;100
Số liền sau số 100là 101 nên ba số tự nhiên liên tiếp là 99;100;101
Vậy cả hai số 98;101đều thỏa mãn yêu cầu đề bài.
Cho hai số tự nhiên 99; 100. Hãy tìm số tự nhiên a để ba số đó lập thành ba số tự nhiên liên tiếp?
A. 98
B. 97
C. 101
D. Cả A và C
Đáp án là D
liền trước số 99 là số 98 nên có ba số tự nhiên liên tiếp là 98; 99; 100.
Số liền sau số 100 là số 101 nên có ba số tự nhiên liên tiếp là 99; 100; 101.
Cho hai số tự nhiên 88;89. Hãy tìm số tự nhiên a để ba số có được tạo thành ba số tự nhiên liên tiếp.
A. 87
B. 90
C. 91
D. Cả A, B đều đúng
Đáp án cần chọn là: D
Số liền trước số 88 là số 87 nên ba số tự nhiên liên tiếp là 87;88;89
Số liền sau số 89 là số 90 nên ba số tự nhiên liên tiếp là 88;89;90
Vậy cả hai số 87;90đều thỏa mãn yêu cầu đề bài.
Cho hai số tự nhiên 99; 100. Hãy tìm số tự nhiên a để ba số đó lập thành ba số tự nhiên liên tiếp?
A. 98
B. 97
C. 101
D. Cả A và C
Đáp án là D
Số liền trước số 99 là số 98 nên có ba số tự nhiên liên tiếp là 98; 99; 100.
Số liền sau số 100 là số 101 nên có ba số tự nhiên liên tiếp là 99; 100; 101.
Câu 9:
Cho hai số tự nhiên 99; 100. Hãy tìm số tự nhiên a để ba số đó lập thành ba số tự nhiên liên tiếp?
A. 98
B .97
C. 101
D. Cả A và C
Câu 9:
Cho hai số tự nhiên 99; 100. Hãy tìm số tự nhiên a để ba số đó lập thành ba số tự nhiên liên tiếp?
A. 98
B .97
C. 101
D. Cả A và C
✔✔a bằng giá trị trung bình cộng của 7,11 và a. Vì vậy a có giá trị bằng trung bình cộng của 7 và 11.
Số tự nhiên a cần tìm là:
(7+11):2=9
Đáp số: a là 9
Cho ba số tự nhiên 7,11 và a. Biết số tự nhiên a bằng trung bình cộng của 3 số tự nhiên đã cho. Tìm số tự nhiên a.
Giải toán bằng sơ đồ đoạn thẳng của tiểu học em nhé
Tổng của hai số 7 và 11 là: 7 + 11 = 18
Coi trung bình cộng của ba số là 1 phần ta có sơ đồ
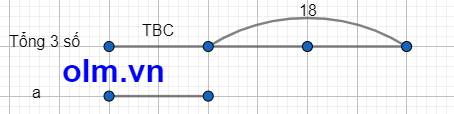
theo sơ đồ ta có:
Số tự nhiên a là: 18 : 2 = 9
Đáp số: 9
a. Tìm hai số tự nhiên liên tieeos có tích bàng 630
b. Tìm ba số tự nhiên liên tiếp có tích bằng 2184
c. Tìm hai số tự nhiên liên tiếp có tích bằng 756
d. Tìm ba số tự nhiên liên tiếp có tích bằng10626
e. Tìm ba số lẻ liên tiếp có tích bằng 1287
b) Gọi 3 số tự nhiên liên tiếp là: a, a+1, a+2 \(\left(a\in N\right)\)
Theo bài ra ta có: \(a\left(a+1\right)\left(a+2\right)=2184\)
\(\Leftrightarrow\)\(a\left(a+1\right)\left(a+2\right)-2184=0\)
\(\Leftrightarrow\)\(\left(a-12\right)\left(a^2+15a+182\right)=0\)
\(\Leftrightarrow\)\(a=12\)
Vậy 3 số tự nhiên liên tiếp đó là: 12, 13, 14
a) Tìm hai số tự nhiên liên tiếp có tích bằng 630
b) Tìm ba số tự nhiên liên tiếp có tích bằng 2184
c) Tìm hai số tự nhiên liên tiếp có tích bằng 756
d) Tìm ba số tự nhiên liên tiếp có tích bằng 10626
e) Tìm ba số tự nhiên liên tiếp có tích bằng 1287
a: Gọi hai só cần tìm là a,a+1
Theo đề, ta có: a(a+1)=630
\(\Leftrightarrow a^2+a-630=0\)
\(\Delta=1^2-4\cdot1\cdot\left(-630\right)=2521\)
=>Không có hai số tự nhiên liên tiếp nào thỏa mãn đề bài
b: Gọi ba số tự nhiên liên tiếp là a;a+1;a+2
Theo đề, ta có:
\(a^3+3a^2+2a-2184=0\)
\(\Leftrightarrow a^3-12a^2+15a^2-180a+182a-2184=0\)
=>a=12
Vậy: Ba số cần tìm là 12;13;14
c: Gọi hai số liên tiếp là a,a+1
Theo đề,ta có: a(a+1)=756
\(\Leftrightarrow a^2+a-756=0\)
\(\Delta=1^2+4\cdot1\cdot756=3025\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}a_1=\dfrac{-1-55}{2}=-\dfrac{56}{2}=-28\left(loại\right)\\a_2=\dfrac{-1+55}{2}=27\left(nhận\right)\end{matrix}\right.\)
Vậy: Hai số cần tìm là 27 và 28
Tìm số tự nhiên có ba chữ số Tìm số tự nhiên a b c biết 1 + 2 + 3 + . . . + b c = a b c .
Ta có: 1+2+3+...+bc=abc (0 < a ≤9 và 0≤b,c ≤9)
<=> ab ( \(ab\) +1)2 = abc
<=> bc ( bc+1)=2. abc
<=> bc.bc+bc=2(100a+bc)
<=> bc.bc+bc=200a+2bc
<=> bc(bc-1)=200a
Nhận xét: Vế phải là 200a => Số tận cùng là 0.
Vậy vế trái bc.(bc-1) cũng phải có tận cùng là 0 và phải chia hết cho 100.
Có các trường hợp: c = 0, c = 1, c = 5 và c = 6.
Xét từng trường hợp, có: +/ TH1: Với c=0 => b0(b0-1)=200a
<=> 10b(10b-1)=200a <=> b(10b-1)=20a. Không có giá trị của b thỏa mãn để: b(10b-1)⋮10 => Loại
+Trường hợp 2: Với c=1 => b1(b1-1)=200a
<=> (10b+1).10b=200a <=> b(10b+1)=20a. Không có giá trị của b thỏa mãn để: b(10b+1)⋮10 => Loại
+/ Trường hợp 3: Với c=5 => b5(b5-1)=200a <=> b4.b5=200a
Nhận thấy: b4 và b5 là 2 số tự nhiên liên tiếp. Để tích của chúng có 2 chữ số tận cùng là 0.
Ta chọn được duy nhất b=2 (Do 24.25=600) => 24.25=200a => a=3 (nhận)
+/ Trường hợp4: Với c=6 => b6.b5=200a
Nhận thấy: b5 và b6 là 2 số tự nhiên liên tiếp. Để tích của chúng có 2 chữ số tận cùng là 0.
Ta chọn được duy nhất b=7 (Do 75.76=5700) <=> 75.76=200a => a=28,5 (Loại)
Vậy cặp số duy nhất thỏa mãn là: a=3, b=2, c=5 Vậy \(\overline{abc}\) = 325.
TTTTTTTTTTTTTTHHHHHHHHHHHHHAAAAAAAAAAAAAANNNNNNNNKKKKKKKKKKKKKKSSSSSSSSSSSSSSS HỒ ĐỨC VIỆT