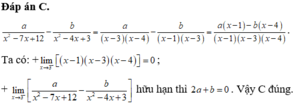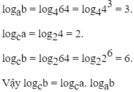cho 2 phân số a/b và a/c . tìm hệ thức liên hệ giữa a;b;c để a/b - a/c = a/b x a/c
NN
Những câu hỏi liên quan
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để
lim
x
→
2
(
a
x
2
-
6
x
+
8
-
b
x
2
-
5...
Đọc tiếp
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để
lim x → 2 ( a x 2 - 6 x + 8 - b x 2 - 5 x + 6 ) là hữu hạn
A. a -2b =0
B. a +b = 0
C. a -3b =0
D. a -b =0
cho A ( 0,-5) B( 1; -3) và C ( x;y) tìm hệ thức liên hệ giữa x và y để b,c thẳng hàng
\(\overrightarrow{AB}=\left(1;2\right)\)
\(\overrightarrow{AC}=\left(x;y+5\right)\)
Để A,B,C thẳng hàng thì x/1=y+5/2
=>2x=y+5
=>y=2x-5
Đúng 0
Bình luận (0)
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để
lim
x
→
2
a
x
2
-
6
x
+
8
-
b...
Đọc tiếp
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để lim x → 2 a x 2 - 6 x + 8 - b x 2 - 5 x + 6 là hữu hạn
A. a-2b = 0
B. a+b = 0
C. a-3b = 0
D. a-b = 0
Cho hai phân số a/b và b/c. Tìm hệ thức giữa a,b,c để cho : a/b -a/c=a/b nhân a/c
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để giới hạn
lim
x
→
3
−
a
x
2
−
7
x
+
12
−...
Đọc tiếp
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để giới hạn lim x → 3 − a x 2 − 7 x + 12 − b x 2 − 4 x + 3 là hữu hạn
A. 4 a + b = 0
B. 3 a + b = 0
C. 2 a + b = 0
D. a + b = 0
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để giới hạn
lim
x
→
3
−
a
x
2
−
7
x
+
12
−
b
x...
Đọc tiếp
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để giới hạn lim x → 3 − a x 2 − 7 x + 12 − b x 2 − 4 x + 3 là hữu hạn.
A. 4 a + b = 0
B. 3 a + b = 0
C. 2 a + b = 0
D. a + b = 0
Đáp án C
a x 2 − 7 x + 12 − b x 2 − 4 x + 3 = a x − 3 x − 4 − b x − 1 x − 3 = a x − 1 − b x − 4 x − 1 x − 3 x − 4
lim x → 3 − x − 1 x − 3 x − 4 = 0
lim x → 3 − a x 2 − 7 x + 12 − b x 2 − 4 x + 3
hữu hạn thì 2 a + b = 0 . Vậy C đúng
Đúng 0
Bình luận (0)
Câu 6. Cho a3 + b3 2. Tìm giá trị lớn nhất của biểu thức: N a + b.Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| |a - b|Câu 9.a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4ab) Cho a, b, c 0 và abc 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8Câu 10. Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2)b) (a + b + c)2 ≤ 3(a2 + b2 + c2)Câu 11. Tìm các giá trị của x sao cho:a) |2x – 3| |1 – x|b) x2 – 4x ≤ 5c) 2x(2x –...
Đọc tiếp
Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|
Câu 9.
a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
Câu 10. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
Câu 11. Tìm các giá trị của x sao cho:
a) |2x – 3| = |1 – x|
b) x2 – 4x ≤ 5
c) 2x(2x – 1) ≤ 2x – 1.
Câu 12. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 13. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Câu 9:
\(a,\left(a+1\right)^2\ge4a\\ \Leftrightarrow a^2+2a+1\ge4a\\ \Leftrightarrow a^2-2a+1\ge0\\ \Leftrightarrow\left(a-1\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=1\)
\(b,\) Áp dụng BĐT cosi: \(\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge2\sqrt{a}\cdot2\sqrt{b}\cdot2\sqrt{c}=8\sqrt{abc}=8\)
Dấu \("="\Leftrightarrow a=b=c=1\)
Câu 10:
\(a,\left(a+b\right)^2\le2\left(a^2+b^2\right)\\ \Leftrightarrow a^2+2ab+b^2\le2a^2+2b^2\\ \Leftrightarrow a^2-2ab+b^2\ge0\\ \Leftrightarrow\left(a-b\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b\)
\(b,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\le3a^2+3b^2+3c^2\\ \Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
Câu 13:
\(M=\left(a^2+ab+\dfrac{1}{4}b^2\right)-3\left(a+\dfrac{1}{2}b\right)+\dfrac{3}{4}b^2-\dfrac{3}{2}b+2021\\ M=\left[\left(a+\dfrac{1}{2}b\right)^2-2\cdot\dfrac{3}{2}\left(a+\dfrac{1}{2}b\right)+\dfrac{9}{4}\right]+\dfrac{3}{4}\left(b^2-2b+1\right)+2018\\ M=\left(a+\dfrac{1}{2}b-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\left(b-1\right)^2+2018\ge2018\\ M_{min}=2018\Leftrightarrow\left\{{}\begin{matrix}a+\dfrac{1}{2}b=\dfrac{3}{2}\\b=1\end{matrix}\right.\Leftrightarrow a=b=1\)
Đúng 3
Bình luận (0)
Câu 6:
$2=(a+b)(a^2-ab+b^2)>0$
$\Rightarrow a+b>0$
$4(a^3+b^3)-N^3=4(a^3+b^3)-(a+b)^3$
$=3(a^3+b^3)-3ab(a+b)=(a+b)(a-b)^2\geq 0$
$\Rightarrow N^3\leq 4(a^3+b^3)=8$
$\Rightarrow N\leq 2$
Vậy $N_{\max}=2$
Đúng 5
Bình luận (0)
Câu 7:
BĐT $\Leftrightarrow a^3+b^3\geq ab(a+b)$
$\Leftrightarrow a^3+b^3-ab(a+b)\geq 0$
$\Leftrightarrow (a-b)^2(a+b)\geq 0$ (luôn đúng với mọi $a,b,c>0$)
Vậy ta có đpcm
Dấu "=" xảy ra khi $a=b>0$, $c$ dương bất kỳ.
Đúng 5
Bình luận (0)
Xem thêm câu trả lời
Cho a = 4, b = 64, c = 2. Tính log a b , log c a , log c b
Tìm một hệ thức liên hệ giữa ba kết quả thu được.
cho 2 p/s a/b và a/c.Tìm hệ thức liên hệ giữa a,b,c sao cho: a/b - a/c = a/b.a/c