Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;3), B(3;4;4), C(2;6;6) và I(a;b;c) là tâm đường tròn ngoại tiếp tam giác ABC. Tính S = a+b+c
A. 63 5
B. 46 5
C. 31 3
D. 10
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A ( 2 ; 3 ; 2 ) , B ( - 2 ; - 1 ; 4 ) . Tìm tọa độ điểm E thuộc trục Oz sao cho E cách đều hai điểm A, B
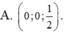
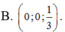
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình: 3x+4y+2z+4=0 và điểm A(1;-2;3). Tính khoảng cách d từ A đến (P)
A. d = 5 9
B. d = 5 29
C. d = 5 29
D. 5 3
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-1;1); B(2;1;-2), C(0;0;1) . Gọi H(x;y;z) là trực tâm của tam giác ABC thì giá trị của x+y+z là kết quả nào dưới đây?
A. 1
B. 1 3
C. 2
D. 3
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi
qua điểm A(1;2;-3) có vectơ pháp tuyến n → = ( 2 ; - 1 ; 3 ) là
A. 2x - y + 3z + 9 = 0
B. 2x -y + 3z - 4 = 0
C. x - 2y - 4 = 0
D. 2x - y + 3z + 4 = 0
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A(1;2;-3) có vectơ pháp tuyến n → = ( 2 ; - 1 ; 3 ) là
A. 2x - y + 3z + 9 = 0
B. 2x - y + 3z - 4 = 0
C. x - 2y - 4 = 0
D. 2x - y + 3z + 4
Trong không gian với hệ tọa độ Oxyz, cho ba điểm
A 0 ; 1 ; 1 , B 3 ; 0 ; - 1 , C 0 ; 21 ; - 19 và mặt cầu
S : x - 1 2 + y - 1 2 + z - 1 2 = 1 ,
M a ; b ; c là điểm thuộc mặt cầu (S) sao cho biểu thức
T = 3 M A 2 + 2 M B 2 + M C 2 đạt giá trị nhỏ nhất. Tính tổng a + b + c
A. a + b + c = 0
B. a + b + c = 12
C. a + b + c = 12 5
D. a + b + c = 14 5
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng ( α ) : x = 1 , ( β ) : y = - 1 , ( γ ) : z = 1 . Bán kính của mặt cầu (S) bằng
A. 33
B. 1
C. 3 2
D. 3
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (2;0;0), B (0;3;0), C (0;0;6), D (1;1;1). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D?
A. 6
B. 10
C. 7
D. 5.
Chọn C
Phương trình mặt phẳng 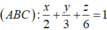
Ta thấy 4 điểm A, B, C, D đồng phẳng (do D ∈ (ABC)).
Chọn 3 trong 5 điểm có ![]()
Chọn 3 trong 4 điểm đồng phẳng A, B, C, D có ![]()
Vậy có 10 - 4 + 1 = 7 => mặt phẳng phân biệt đi qua 5 điểm đã cho.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng (P): 2x + y - 4z + 1 =0. Đường thẳng (d) đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d.
A. x = 1 + 5 t y = 2 - 6 t z = 3 + t
B. x = t y = 2 t z = 2 + t
C. x = 1 + 3 t y = 2 + 2 t z = 3 + t
D. x = 1 - t y = 2 + 6 t z = 3 + t
Trong không gian với hệ trục tọa độ Oxyz cho điểm A(2;-2;2) và mật cầu (S): x 2 + y 2 + ( z - 1 ) 2 = 4 . Điểm M di chuyển trên mặt cầu (S) đồng thời thỏa mãn O M → . A M → = 6 . Điểm M luôn thuộc mặt phẳng nào dưới đây?
![]()
![]()
![]()
![]()