Đáp án B
Phương pháp giải:
Tâm đường tròn ngoại tiếp cách đều 3 đỉnh của tam giác và thuộc mặt phẳng chứa tam giác
Lời giải:
Ta có A B → = ( 2 ; 2 ; 1 ) A C → = ( 1 ; 4 ; 3 ) ⇒ A B → ; A C → = ( 2 ; - 5 ; 6 ) => Phương trình (ABC): 2x – 5y + 6z – 10 = 0
Vì I(a;b;c) là tâm đường tròn ngoại tiếp ∆ABC 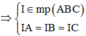
Lại có 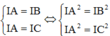
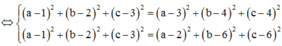
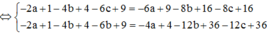
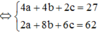
Kết hợp với ![]()
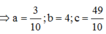 . Vậy S =
46
5
. Vậy S =
46
5

