Tính giá trị của biểu thức trong mỗi trường hợp sau:
a) \( - 6x - 12\) với \(x = - 2\);
b) \( - 4y + 20\) với \(y = - 8\).
Tính giá trị của biểu thức P = (-35).x - (-15).37 trong mỗi trường hợp sau:
a) x = 15;
b) x = - 37.
a) Thay x = 15 ta được:
P = (-35).x - (-15).37 = (-35).15 - (-15).37
= (-35).15 + 15.37 = 15.[(-35) +37] = 15.2 = 30.
b) Thay x = -37 ta được:
P = (-35).(-37) - (-15).37 = 35.37 + 15.37
= 37.(15 + 35) = 37.50 = 1850.
Tính giá trị của biểu thức trong mỗi trường hợp sau:
a) 2x, biết x = -8;
b) -7y, biết y = 6;
c) -8z - 15, biết z = -4.
a) Thay x = - 8 => 2 . (- 8) = - (2 . 8) = - 16.
b) Thay y = 6 => (- 7) . 6 = - (7 . 6) = - 36.
c) Thay z = - 4 => – 8 . (- 4) – 15 = - (8 . 4) – 15 = 32 – 15 = 17.
a) Thay x=-8 vào biểu thức 2x, ta được:
\(2\cdot\left(-8\right)=-16\)
b) Thay y=6 vào biểu thức -7y, ta được:
\(-7\cdot6=-42\)
c) Thay z=-4 vào biểu thức -8z-15, ta được:
\(\left(-8\right)\cdot\left(-4\right)-15=32-15=17\)
Tính giá trị của biểu thức 16 x 2 – 24x + 9 trong mỗi trường hợp sau:
a) x = 0; b) x = 1 4 ; c) x = 12; d) x = 3 4 ;
Vì A = 16 x 2 – 24 + 9 = ( 4 x – 3 ) 2 nên:
a) x= 0 thì A = 9; b) x = 1 4 thì A = 4;
c) x = 12 thì A = 2025; d) x = 3 4 thì A = 0.
Cho x = -12. Tính giá trị của mỗi biểu thức sau:
a) 18 + |x|
b) 25 - |x|
c) |3+x| - |7|
Vì x = -12 nên |x| = 12
a) 18 + |x| = 18 + 12 = 30;
b) 25 - |x| = 25 – 12 = 13;
c) |3+x| - |7| = |3 + (-12)| - 7 = | 3+(-12)| - 7 = |-9| - 7 = 9 – 7 = 2
a: 18+|x|=18+12=30
b: 25-|x|=25-12=13
c: |3+x|-|7|=|3-12|-7=9-7=2
tính giá trị lớn nhất và giá trị nhỏ nhất của các biểu thức sau:
a) A= 1-8x-x^2
b) B= 5-2x+x^2
c) C= x^2+4y^2-6x+8y-2021
a) \(A=1-8x-x^2=-\left(x^2+8x+16\right)+17=-\left(x-4\right)^2+17\le17\)
\(ĐTXR\Leftrightarrow x=4\)
b) \(B=5-2x+x^2=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
\(ĐTXR\Leftrightarrow x=1\)
c) \(C=x^2+4y^2-6x+8y-2021=\left(x^2-6y+9\right)+\left(4y^2+8y+4\right)-2034=\left(x-3\right)^2+\left(2y+2\right)^2-2034\ge-2034\)
\(ĐTXR\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
a: Ta có: \(A=-x^2-8x+1\)
\(=-\left(x^2+8x-1\right)\)
\(=-\left(x^2+8x+16-17\right)\)
\(=-\left(x+4\right)^2+17\le17\forall x\)
Dấu '=' xảy ra khi x=-4
b: Ta có: \(x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
Cho biểu thức \(A=2x+3\sqrt{4-x}+1\). Trong mỗi trường hợp sau hãy thay x bởi giá trị đã cho rồi tính giá trị của biểu thức:
a) Trường hợp x = - 5
b) Trường hợp x = 5
ĐKXĐ: x<=4
a: Thay x=-5 vào A, ta được:
\(A=2\cdot\left(-5\right)+3\cdot\sqrt{4+5}+1=-10+1+3\cdot3=0\)
b: Vì x=5 không thỏa mãn ĐKXĐ nên khi x=5 thì A không có giá trị
Cho biểu thức:
\(P=\dfrac{x-\sqrt{x}}{x-9}+\dfrac{1}{\sqrt{x}+3}-\dfrac{1}{\sqrt{x}-3};x\ge0,x\ne9\)
1) Rút gọn biểu thức P.
2) Tính giá trị của P trong các trường hợp sau:
a) \(x=\dfrac{9}{4}\)
b) \(x=\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\)
3) Tìm x để \(\dfrac{1}{P}>\dfrac{5}{4}\)
1: Ta có: \(P=\dfrac{x-\sqrt{x}}{x-9}+\dfrac{1}{\sqrt{x}+3}-\dfrac{1}{\sqrt{x}-3}\)
\(=\dfrac{x-\sqrt{x}+\sqrt{x}-3-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\)
2)
a) Thay \(x=\dfrac{9}{4}\) vào P, ta được:
\(P=\left(\dfrac{3}{2}+2\right):\left(\dfrac{3}{2}+3\right)=\dfrac{7}{2}:\dfrac{11}{2}=\dfrac{7}{11}\)
b) Ta có: \(x=\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\)
\(=5+\sqrt{2}-4-\sqrt{2}\)
=1
Thay x=1 vào P, ta được:
\(P=\dfrac{1+2}{1+3}=\dfrac{3}{4}\)
Tính giá trị của mỗi biểu thức sau:
a) 250 + 250 x 2
(250 + 250) x 2
b) 750 – 50 x 5
(750 – 50) x 5
c) 210 x 4 – 4 x 210
3 x (270 : 9) x 0
a) \(250 + 250 × 2 = 250 + 500 = 750 \\ (250 + 250) × 2 = 500 × 2 = 1 000\)
b)\( 750 – 50 × 5 = 750 – 250 = 500\\
(750 – 50) × 5 = 700 × 5 = 3 500\)
c) \(210 × 4 – 4 × 210 = 840 – 840 = 0\\
3 × (270 : 9) × 0 = 0\)
Tính giá trị của biểu thức 49x2 – 70x + 25 trong mỗi trường hợp sau:
a) x = 5
b) x = 1/7
A = 49x2 – 70x + 25
= (7x)2 – 2.7x.5 + 52
= (7x – 5)2
a) Với x = 5: A = (7.5 – 5)2 = 302 = 900
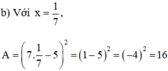
Tìm giá trị( LN ) giá trị nhỏ nhất ( gtnn) của các biểu thức sau:
A) A= x^2+3x+1
B) B= 2x^2+6x+y^2+2xy+12
C) C= 2x-x^2
\(A=\left(x^2+2\cdot\dfrac{3}{2}x+\dfrac{9}{4}\right)-\dfrac{5}{4}=\left(x+\dfrac{3}{2}\right)^2-\dfrac{5}{4}\ge-\dfrac{5}{4}\\ A_{min}=-\dfrac{5}{4}\Leftrightarrow x=-\dfrac{3}{2}\\ B=\left(x^2+2xy+y^2\right)+\left(x^2+6x+9\right)+3\\ B=\left(x+y\right)^2+\left(x+3\right)^2+3\ge3\\ B_{min}=3\Leftrightarrow\left\{{}\begin{matrix}x+y=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-3\end{matrix}\right.\\ C=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1\le1\\ C_{max}=1\Leftrightarrow x=1\)