Giải các phương trình sau. Làm tròn kết quả đến hàng phần nghìn.
a) \({3^{x + 2}} = 7\);
b) \({3.10^{2x + 1}} = 5\).
H24
Những câu hỏi liên quan
VD: làm tròn 24,037 đến hàng phần mười ta được kết quả là 24,0 24,037 hàng làm tròn giữ nguyên 35 bỏ đi các chữ số sau hàng làm tròn bài tập : làm tròn số 3,14159 đến hàng phần nghìn (mk cần lời giải gấp , mn giúp mk vs ngày là mk phải giao bài lại cho cô r )
Đọc tiếp
mình nhầm bạn ơi,phải là 3,142 mới đúng nhé:((
Đúng 1
Bình luận (0)
H24
2 tháng 3 2022 lúc 15:25
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là:92,1
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:-845,7
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là:-72,9
Đúng 1
Bình luận (0)
\(92,117\approx92,12\\ -845,654\approx-845,65\approx-845,7\\ 82,572\approx82,57\\ 82,572\approx82,57\\ -72,882\approx-72,9\)
Đúng 1
Bình luận (0)
Giải phương trình 3 2 x - 3 = 7 . Viết nghiệm dưới dạng thập phân, làm tròn đến hàng phần nghìn.
A. x ≈ 2,38
B. x ≈ 2,386
C. x ≈ 2,384
D. x ≈ 1,782
Đưa các phương trình sau về dạng ax2 + 2b'x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):
3x2 + 3 = 2(x + 1)
3x2 + 3 = 2(x + 1)
⇔ 3x2 + 3 = 2x + 2
⇔ 3x2 + 3 – 2x – 2 = 0
⇔ 3x2 – 2x + 1 = 0
Phương trình có a = 3; b’ = -1; c = 1; Δ’ = b’2 – ac = (-1)2 – 3.1 = -2 < 0
Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Đưa các phương trình sau về dạng ax2 + 2b'x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai): 0,5x(x + 1) = (x – 1)2
0,5x(x + 1) = (x – 1)2
⇔ 0,5x2 + 0,5x = x2 – 2x + 1
⇔ x2 – 2x + 1 – 0,5x2 – 0,5x = 0
⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0
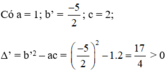
Phương trình có hai nghiệm phân biệt:
Đúng 0
Bình luận (0)
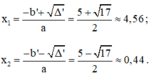
Em hãy tính hóa đơn tiền điện của bạn Nam, biết chỉ số cũ là 335, chỉ số mới là 339. Đơn giá là 6200 đồng. Kết quả làm tròn đến chữ số hàng nghìn.
A/. 23000 B/. 24000 C/. 25000 D/. 26000
Giúp mk câu này vs!!!!!!!!!!!!!!!!!!!
Đưa các phương trình sau về dạng ax2 + 2b'x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):
(2x - √2)2 – 1 = (x + 1)(x – 1)
(2x - √2)2 – 1 = (x + 1)(x – 1);
⇔ 4x2 – 2.2x.√2 + 2 – 1 = x2 – 1
⇔ 4x2 – 2.2√2.x + 2 – 1 – x2 + 1 = 0
⇔ 3x2 – 2.2√2.x + 2 = 0
Có: a = 3; b’ = -2√2; c = 2; Δ’ = b’2 – ac = (-2√2)2 – 3.2 = 2 > 0
Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là:
Đúng 0
Bình luận (0)
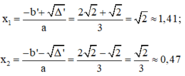
Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm.
a) 3x – 11 = 0
b) 12 + 7x = 0
c) 10 – 4x = 2x – 3
a) \(3x-11=0\)
\(\Rightarrow3x=11\Rightarrow x=\dfrac{11}{3}\approx3,667\)
b) \(12+7x=0\)
\(\Rightarrow7x=-12\Rightarrow x=-\dfrac{12}{7}\approx-1,714\)
c) \(10-4x=2x-3\)
\(\Rightarrow2x+4x=10+3\Rightarrow6x=13\Rightarrow x=\dfrac{13}{6}\approx2,167\)
Đúng 2
Bình luận (0)
H24
2 tháng 3 2022 lúc 15:21
Làm tròn số 92,117 đến hàng phần mười được kết quả là:Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:Làm tròn số 82,572 đến hàng phần mười được kết quả :Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả làLàm tròn số -7671,08 đến hàng chục được kết quả làLàm tròn số 86427 đến hàng trăm được kết quả là:Làm tròn số 28,1 đến hàng đơn vị được kết quả là:Làm tròn số -28,7 đến hàng đơn vị được kết quả làLàm tròn số 128,5 đến hàng chục được kết quả...
Đọc tiếp
Làm tròn số 92,117 đến hàng phần mười được kết quả là:
Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:
Làm tròn số 82,572 đến hàng phần mười được kết quả :
Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là
Làm tròn số -7671,08 đến hàng chục được kết quả là
Làm tròn số 86427 đến hàng trăm được kết quả là:
Làm tròn số 28,1 đến hàng đơn vị được kết quả là:
Làm tròn số -28,7 đến hàng đơn vị được kết quả là
Làm tròn số 128,5 đến hàng chục được kết quả là:
Làm tròn số 28,23 đến hàng đơn vị được kết quả là:
Làm tròn số 5960,12 đến hàng trăm được kết quả là
Làm tròn số -2367,785 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số 327,7892 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số -29670 đến hàng nghìn được kết quả là:
Làm tròn số 7476,5 đến hàng đơn vị được kết quả là
Làm tròn số 4568,12 đến hàng trăm được kết quả là:
Làm tròn số -28,39 đến hàng phần mười được kết quả là:
Làm tròn số -67,193 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số -18,119 đến chữ số thập phân thứ hai được kết quả là
Làm tròn số -15427,99 đến hàng trăm được kết quả là:
