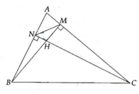
Cho tam giác nhọn ABC không cân nội tiêp (O;R), có H là trực tâm. I, K làn lượt là đường cao kẻ từ A, B. M là trung điểm BC. Kẻ HJ vuông góc với AM.
a) Cm: Góc IHK = góc MJK
b) Cm: \(\Delta AJK\) đồng dạng với \(\Delta ACM\)
c) Cm: MJ . MA < R2
NT
Những câu hỏi liên quan
cho tam giác ABC nhọn trực tâm H nội tp đg tròn (O) Gọi H' là điểm đối xứng của H qua BC CM
a, tg ABH'C là tg nội tiêp
b.bán kính đg tròn ngoại tiếp tam giác BHC = bk đg tròn ngoạn tp tam giác ABC
giúp tớ với tớ đang cần gấp
Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là những tứ giác nội tiêp
Xét tứ giác AMHN có: A M H ^ + A N H ^ = 90 0 + 90 0 = 180 0 => Đpcm
Xét tứ giác BNMC có: B N C ^ = B M C ^ = 90 0 => Đpcm
Đúng 1
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm o các đường cao BE và CF cắt nhau tại H
a) CM tứ giác AEHF và BCEF nội tiêp đg tròn
b) Vẽ đường kính AD và M là trung điểm BC. CM H,M,D thẳng hàng.
(mình cần câu b)
a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b; góc ABD=1/2*180=90 độ
=>BD vuông góc AB
=>BD//CH
góc ACD=1/2*180=90 độ
=>CD vuông góc AC
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
=>BHCD là hbh
=>BC cắt HDtại trung điểm của mỗi đường
=>H,M,D thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB<AC) có 3 góc nhọn nội tiêp (O). Hai đường cao AD và CE cắt nhau tại H
a> C/m BEHD, ACDE nội tiêp
b> Đường thẳng AD cắt (O) tai K khác A. C/m HD=KD
c> Gọi M là tr.điểm của BC, đường thẳng BM căt cung nhỏ BC tại N. C/m goc BCN = goc CAN
Cho tam giác nhọn ABC có các đường cao kẻ từ B, C cắt nhau tại O. CMR: Nếu đường tròn nội tiếp tam giác OAB và đường tròn nội tiếp tam giác OAC có bán kính bằng nhau thì tam giác ABC là tam giác cân.
cho tam giác ABC nhọn nội tiếp (o). Hai đường cao AM và BN cắt nhau tại H và cắt đường tròn (o) lần lượt tại D và E
CMR: a) tứ giác HMCN nội tiếp đường tròn
b) CD=CE
c)tam giác BHD cân
a: Xét tứ giác HMCN co
góc HMC+góc HNC=180 đô
=>HMCN là tứ giác nội tiếp
b: góc CBE=1/2*sđ cung CE
góc CAD=1/2*sđ cung CD
mà góc CBE=góc CAD
nên CE=CD
c: góc BHD=góc ACB=1/2*sđ cung AB=góc BDH
=>ΔBHD cân tại B
Đúng 1
Bình luận (0)
cho tam giác ABC nhọn nội tiếp (o). Hai đường cao AM và BN cắt nhau tại H và cắt đường tròn (o) lần lượt tại D và E
cho tam giác ABC nhọn nội tiếp đường tròn (O). Hai đường cao AM ,BN cắt nhau tại H và cắt đường tròn (O) lần lượt tại D,E. chứng minh rằng
a. tứ giác HMCN nội tiếp đường tròn
b. CD=CE
c. tam giác BHD cân
a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CAD=góc NBC
=>1/2*sđ cung CD=1/2*sđ cung CE
=>CD=CE
c: góc BHM=góc BCN=1/2*sđ cung BA
góc BDH=1/2*sđ cung BA
=>góc BHD=góc BDH
=>ΔBHD cân tại B
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O;R), có các đường cao AI, BK cắt nhau tại H. Hơn nữa, AI, BK cắt đường tròn (O) tương ứng D và E
a) Chứng minh tứ giác AKIB nội tiếp
b) Chứng minh : BHD là tam giác cân
a: Xét tứ giác AKIB có
góc AKB=góc AIB=90độ
=>AKIB là tứ giác nội tiếp
b: góc BHD=góc AHE=90 độ-góc HAC=90 độ-1/2*sđ cung CD
góc BDH=90 độ-góc IBD=90 độ-1/2*sđ cung CD
=>góc BHD=góc BDH
=>ΔBHD cân tại B
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp (O) các đường cao BD và CE cắt nhau tại H .Nếu góc ACB =60° .Chứng minh tam giác HOC cân