Cho hình vuông ABCD, E;F lần lượt là trung điểm AB, BC. CM : a) CE vuông góc với DF b) Gọi m là giao điểm của CE và DF. Chứng minh AM=AD.
NB
Những câu hỏi liên quan
Cho hình vuông ABCD. Dựng điểm E nằm trong hình vuông ABCD sao cho tam giác ABE đều, điểm F nằm ngoài hình vuông ABCD sao cho tam giác FBC đều.
Chứng minh rằng D, E, F thẳng hàng
vì tam giác ABE đều nên góc ABE = AEB = 600
suy ra goc EBC = 90 - 30 = 600
vì tam giác BFC đều nên goc FBC = FCB = 60o
Ta có tam giác EBF cân tại B (vì BE =BF ) và goc EBF = EBC + CBF = 60+30 = 90o
suy ra goc BEF = \(\frac{180-90}{2}\)=45o
ta có goc AEF = AEB + BEF = 60 + 45 = 105o
ta có tam giac AED cân tại A(vì AD = AE) và goc EAD = 30o nên goc AED = \(\frac{180-30}{2}\)= 75o
Ta có goc AED + goc AEF = 75 + 105 = 180o
suy ra D, E, F thẳng hàng
Đúng 0
Bình luận (0)
cho hình vuông abcd trên dc ta lấy điểm e sao cho dt bằng 1/3 dc biết diện tích hình tam giác abe là 5,36 cm2 tính diện tích hình vuông abcdcho hình vuông abcd trên dc ta lấy điểm e sao cho dt bằng 1/3 dc biết diện tích hình tam giác abe là 5,36 cm2 tính diện tích hình vuông abcdcho hình vuông abcd
CHO hình vuông ABCD có đường chéo AC=5V2 .TÍNH DIỆN TÍCH HÌNH VUÔNG ABCD AI GIÚP E VỚI Ạ
Áp dụng đ/l pytago vào Δ vuông ABC tại B ta có :
\(AC^2=AB^2+BC^2\)
mà AB=BC nên ta có :
\(\Leftrightarrow\left(5\sqrt{2}\right)^2=AB^2+AB^2\)
\(\Leftrightarrow50=2AB^2\)
\(\Leftrightarrow AB^2=50:2=25\)
\(\Leftrightarrow AB=\sqrt{25}=5\)( đơn vị diện tích theo đề bạn )
\(S_{hìnhvuông}=a^2=5^2=25\)
còn 1 cách nữa nhưng cách này dễ hiểu hơn á .
Đúng 1
Bình luận (0)
dựa theo cái tính chất hình vuôg mà lm
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh 10m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng
4
5
diện tích vuông ABCD A. Điểm E ở trên cạnh AB sao cho BE 4 m B. Điểm E ở trên cạnh AB sao cho BE 6 m C. Điểm E ở trên cạnh AB sao cho BE 5 m D. Điểm E là trung điểm của AB
Đọc tiếp
Cho hình vuông ABCD có cạnh 10m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng 4 5 diện tích vuông ABCD
A. Điểm E ở trên cạnh AB sao cho BE = 4 m
B. Điểm E ở trên cạnh AB sao cho BE = 6 m
C. Điểm E ở trên cạnh AB sao cho BE = 5 m
D. Điểm E là trung điểm của AB
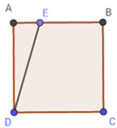
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 102 = 100 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = ( B E + D C ) B C 2 = ( x + 10 ) .10 2 = 5 (x+10)
Vì diện tích hình thang vuông BCDE bằng 4 5 diện tích hình vuông ABCD nên ta có:
SBCDE = SABCD = 5(x + 10) = 4 5 .100 óx + 10 = 16 ó x = 6 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 6 m.
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh 20 m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng
3
4
diện tích vuông ABCD A. Điểm E ở trên cạnh AB sao cho BE 8 m B. Điểm E ở trên cạnh AB sao cho BE 6 m C. Điểm E ở trên cạnh AB sao cho BE 12 m D. Điểm E là trung điểm của AB
Đọc tiếp
Cho hình vuông ABCD có cạnh 20 m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng 3 4 diện tích vuông ABCD
A. Điểm E ở trên cạnh AB sao cho BE = 8 m
B. Điểm E ở trên cạnh AB sao cho BE = 6 m
C. Điểm E ở trên cạnh AB sao cho BE = 12 m
D. Điểm E là trung điểm của AB
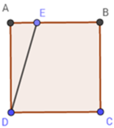
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 202 = 400 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = ( B E + D C ) B C 2 = ( x + 20 ) .20 2 = 10(x + 20)
Vì diện tích hình thang vuông BCDE bằng 3 4 diện tích hình vuông ABCD nên ta có:
SBCDE = 3 4 SABCD = 10(x + 20) = 3 4 .400 óx + 20 = 30 ó x = 10 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 10 m hay E là trung điểm đoạn AB.
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho hình vuông ABCD, E,F thuộc AB (A nằm giữa E và F). Bên trong hình vuông ABCD vẽ hình vuông EFGH, AG cắt HB tại O. Tính khoảng cách từ O đến CD biết AB =6cm, EF = 4cm
Cho hình vuông ABCD có tâm I. Trên tia BC lấy điểm E sao cho BE = AI.
a) Xác định một phép dời hình biến A thành B và I thành E
b) Dựng ảnh của hình vuông ABCD qua phép dời hình ấy.
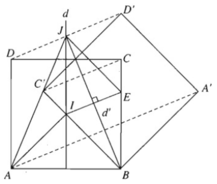
Gọi F là phép đối xứng qua đường trung trực d của cạnh AB, G là phép đối xứng qua đường trung trực d' của cạnh IE. Khi đó F biến AI thành BI, G biến BI thành BE. Từ đó suy ra phép dời hình có được bằng cách thực hiện liên tiếp hai phép biến hình F và G sẽ biến AI thành BE.
Hơn nữa gọi J là giao của d và d', thì dễ thấy JA = JB, JI = JE và 2(JI, JB) = (JI, JE) = 45 ο
(vì JE / /IB). Do đó theo kết quả của bài 1.21, phép dời hình nói trên chính là phép quay tâm J góc 45 ο
Lưu ý. Có thể tìm được nhiều phép dời hình biến AI thành BE.
b) F biến các điểm A, B, C, D thành B, A, D, C; G biến các điểm B, A, D, C thành B, A', D', C'. Do đó ảnh của hình vuông ABCD qua phép dời hình nói trên là hình vuông BA'D'C' đối xứng với hình vuông BADC qua d'
Đúng 0
Bình luận (0)
cho hình vuông ABCD .E nằm trong hình vuông sao cho tam giác ABE là tam giác đều và tam giác ECD cân tại E
Hình vuông ABCD có cạnh 6 cm. Trên đoạn BD lấy điểm E và P sao cho BE = EP = PD.
a) Tính diện tích hình vuông ABCD.
Cho hình vuông ABCD có tâm I. Trên tia BC lấy điểm E sao cho BE = AI
a) Xác định một phép dời hình biến A thành B và I thành E
b) Dựng ảnh của hình vuông ABCD qua phép dời hình ấy





