Cho đường tròn (I) nội tiếp tam giác ABC, tiếp xúc với các cạnh BC, CA, AB lần lượt tại
A’; B’; C’. Tính các độ dài AB’, BC’, CA’ theo các cạnh BC = a; CA = b; AB = c.
Trong hình bên:
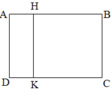
c) Cạnh AB vuông góc với các cạnh: ..........................................
cho hình thang ABCD (AB//CD) có các tia phân giác của các góc C và D gặp nhau tại điểm I thuộc cạnh đáy AB,
Chứng minh rằng AB bằng tổng của hai cạnh bên
Ta có AB // CD => Góc IDC=Góc DIA ( so le trong )
Mà góc IDC=góc IDA ( do ID là tia phân giác góc ADC)
=> Góc DIA= Góc IDA => tam giác DIA cân tại A
=> AD = AI (1)
Ta có AB // CD => Góc DCI = Góc CIB (so le trong )
Mà góc DCI = góc ICB ( do IC là tia phân giác góc DCB)
=> Góc CIB = Góc ICB => tam giác CIB cân tại B
=> BC = BI (2)
Cộng (1) và (2) , vế theo vế .Ta được:
AD + BC = AI + BI
=> AD + BC = AB (đpcm)
Đúng 2
Bình luận (0)
cho hinh thang ABCD (AB//CD) chung minh rang neu hai tia phan giac cua hai goc A va D cung di qua trung diem F cua canh ben BC thi canh ben AD bang tong hai day
Đúng 0
Bình luận (0)
Vì AB//CD ⇒ˆA2=ˆK1⇒A2ˆ=K1ˆ⇒A2^=K1^ (2 góc so le trong). Mà AK là phân giác ˆBAD⇒ˆA1=ˆA2BADˆ⇒A1ˆ=A2ˆBAD^⇒A1^=A2^. Do đó, ˆA1=ˆK1⇒ΔADKA1ˆ=K1ˆ⇒ΔADKA1^=K1^⇒ΔADK cân tại D => AD=KD. (1)
Ta lại có: AB//CD ⇒ˆB2=ˆK2⇒B2ˆ=K2ˆ⇒B2^=K2^ (2 góc so le trong). Mà BK là phân giác ˆABC⇒ˆB1=ˆB2ABCˆ⇒B1ˆ=B2ˆABC^⇒B1^=B2^. Do đó ˆB1=ˆK2⇒ΔBCKB1ˆ=K2ˆ⇒ΔBCKB1^=K2^⇒ΔBCK cân tại C => BC=KC. (2)
Từ (1) và (2) => AD+BC=KD+KC.
Mặt khác K∈CDK∈CDK∈CD => CD=KD+KC => CD=AD+BC => đpcm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC. Trên cạnh AB,AC lần lượt lấy các điểm B', C' sao có AB'/AB = AC'AC. Qua B' vẽ đường thẳng a song song với BC cắt cạnh AC tại C''
a) So sánh độ dài các đoạn thằng AC' và AC''
b) Chứng minh B'C' // BC
Lời giải :
Ta có : \(\frac{AB'}{AB}=\frac{AC'}{AC}\)( GT ) ( 1 )
+) Đường thẳng a đi qua B' song song với BC ( GT )
\(B'C''//BC\)( vì đường thẳng a cắt AC tại C'' )
\(\Rightarrow\frac{AB'}{AB}=\frac{AC''}{AC}\)( Định lí Ta lét ) ( 2 )
Từ ( 1 ) và ( 2 )
\(\Rightarrow AC'=AC''\)
Cho tam giác ABC. Trên các cạnh AB, AC lần lượt lấy các điểm B', C'. Chứng minh S ABC / S AB'C' = AB/AB' . CH/C'H'
Cho tam giác ABC.Trên các cạnh AB,AC lần lượt lấy các điểm B’,C’ sao choAB'/AB=AC'/AC.Qua B’ vẽ đường thẳng a song song BC,cắt cạnh AC tại C”.
a)So sánh độ dài các đoạn thẳng AC’ và AC”
b)Chứng minh:B’C’// BC
Cho hình chữ nhật ABCD . Trên cạnh AB lấy 5 điểm và trên cạnh CD lấy 6 điểm . Nối đỉnh C và đỉnh D với mỗi điểm thuộc cạnh AB. Nối đỉnh A và đỉnh B với mỗi điểm thuộc cạnh CD . Hỏi có bao nhiêu tam giác có các đỉnh nằm trên các cạnh của hình chữ nhật được tạo thành
Cho tam giác ABC vuông tại A, có các cạnh góc vuông AB=15, AC=20. Từ C kẻ đường vuông góc với cạnh huyền, đường này cắt đường thẳng AB tại D. Tính AB và CD
Cho lăng trụ ABC.A′B′C′ có tất cả các cạnh bằng 1, hình chiếu vuông góc của A′ lên mặt phẳng (ABC) trùng với trung điểm cạnh AB. Côsin góc giữa hai mặt phẳng (A′BC) và (AB′C′) bằng A.
65
65
B.
2
26
13
C.
143
13
D.
65...
Đọc tiếp
Cho lăng trụ ABC.A′B′C′ có tất cả các cạnh bằng 1, hình chiếu vuông góc của A′ lên mặt phẳng (ABC) trùng với trung điểm cạnh AB. Côsin góc giữa hai mặt phẳng (A′BC) và (AB′C′) bằng
A. 65 65
B. 2 26 13
C. 143 13
D. 65 13
Gọi O là trung điểm cạnh
A
B
⇒
A
'
O
⊥
(
A
B
C
)
và 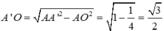 Lập hệ trục toạ độ Oxyz với các tia Ox, Oy, Oz lần lượt trùng với các tia OC, OB, OA’. Toạ độ các đỉnh là o(0;0;0),
Lập hệ trục toạ độ Oxyz với các tia Ox, Oy, Oz lần lượt trùng với các tia OC, OB, OA’. Toạ độ các đỉnh là o(0;0;0),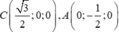

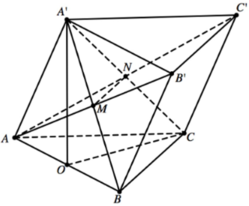
Suy ra ![]()
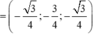
Và
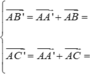
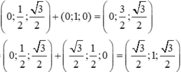
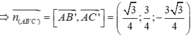
Vậy ![]()
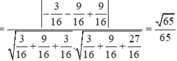
Chọn đáp án A.
Cách 2: Có thể dùng công thức thể tích tứ diện cho TH đặc biệt:
![]()
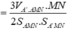
Chọn đáp án A.
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=5cm,AC=7cm,BC=9cm.Hãy tính độ dài các cạnh của tam giác A'B'C' đồng dạng với tam giác đã cho biết cạnh A'B' tương ứng với cạnh AB và lớn hơn cạnh đó 3cm
Theo giả thiết ta có: \(A'B'=AB+3=5+3=8\left(cm\right)\).
Do \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}\)
\(\Rightarrow\dfrac{7}{A'C'}=\dfrac{9}{B'C'}=\dfrac{5}{8}\Rightarrow\left\{{}\begin{matrix}A'C'=\dfrac{7.8}{5}=\dfrac{56}{5}\left(cm\right)\\B'C'=\dfrac{9.8}{5}=\dfrac{72}{5}\left(cm\right)\end{matrix}\right.\).
Đúng 2
Bình luận (0)



